Reconstruction with Constrained Spherical Deconvolution¶
This example shows how to use Constrained Spherical Deconvolution (CSD) introduced by Tournier et al. [Tournier2007].
This method is mainly useful with datasets with gradient directions acquired on a spherical grid.
The basic idea with this method is that if we could estimate the response function of a single fiber then we could deconvolve the measured signal and obtain the underlying fiber distribution.
In this way, the reconstruction of the fiber orientation distribution function (fODF) in CSD involves two steps:
Estimation of the fiber response function
Use the response function to reconstruct the fODF
Let’s first load the data. We will use a dataset with 10 b0s and 150 non-b0s with b-value 2000.
import numpy as np
from dipy.data import fetch_stanford_hardi, read_stanford_hardi, default_sphere
fetch_stanford_hardi()
img, gtab = read_stanford_hardi()
data = img.get_data()
You can verify the b-values of the dataset by looking at the attribute
gtab.bvals. Now that a datasets with multiple gradient directions is
loaded, we can proceed with the two steps of CSD.
## Step 1. Estimation of the fiber response function.
There are many strategies to estimate the fiber response function. Here two different strategies are presented.
Strategy 1 - response function estimates from a local brain region
One simple way to estimate the fiber response function is to look for regions
of the brain where it is known that there are single coherent fiber
populations. For example, if we use an ROI at the center of the brain, we will
find single fibers from the corpus callosum. The auto_response function
will calculate FA for an ROI of radius equal to roi_radius in the center
of the volume and return the response function estimated in that region for
the voxels with FA higher than 0.7.
from dipy.reconst.csdeconv import auto_response
response, ratio = auto_response(gtab, data, roi_radius=10, fa_thr=0.7)
The response tuple contains two elements. The first is an array with
the eigenvalues of the response function and the second is the average S0 for
this response.
It is good practice to always validate the result of auto_response. For
this purpose we can print the elements of response and have a look at their
values.
print(response)
(array([ 0.0014, 0.00029, 0.00029]), 416.206)
The tensor generated from the response must be prolate (two smaller eigenvalues should be equal) and look anisotropic with a ratio of second to first eigenvalue of about 0.2. Or in other words, the axial diffusivity of this tensor should be around 5 times larger than the radial diffusivity.
print(ratio)
0.21197
We can double-check that we have a good response function by visualizing the response function’s ODF. Here is how you would do that:
from dipy.viz import window, actor
from dipy.sims.voxel import single_tensor_odf
# Enables/disables interactive visualization
interactive = False
ren = window.Renderer()
evals = response[0]
evecs = np.array([[0, 1, 0], [0, 0, 1], [1, 0, 0]]).T
response_odf = single_tensor_odf(default_sphere.vertices, evals, evecs)
# transform our data from 1D to 4D
response_odf = response_odf[None, None, None, :]
response_actor = actor.odf_slicer(response_odf, sphere=default_sphere,
colormap='plasma')
ren.add(response_actor)
print('Saving illustration as csd_response.png')
window.record(ren, out_path='csd_response.png', size=(200, 200))
if interactive:
window.show(ren)
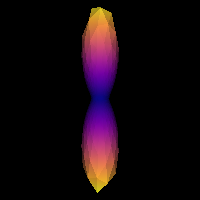
Estimated response function.¶
ren.rm(response_actor)
Strategy 2 - data-driven calibration of response function Depending on the dataset, FA threshold may not be the best way to find the best possible response function. For one, it depends on the diffusion tensor (FA and first eigenvector), which has lower accuracy at high b-values. Alternatively, the response function can be calibrated in a data-driven manner [Tax2014].
First, the data is deconvolved with a ‘fat’ response function. All voxels that are considered to contain only one peak in this deconvolution (as determined by the peak threshold which gives an upper limit of the ratio of the second peak to the first peak) are maintained, and from these voxels a new response function is determined. This process is repeated until convergence is reached. Here we calibrate the response function on a small part of the data.
from dipy.reconst.csdeconv import recursive_response
A WM mask can shorten computation time for the whole dataset. Here it is created based on the DTI fit.
import dipy.reconst.dti as dti
tenmodel = dti.TensorModel(gtab)
tenfit = tenmodel.fit(data, mask=data[..., 0] > 200)
from dipy.reconst.dti import fractional_anisotropy
FA = fractional_anisotropy(tenfit.evals)
MD = dti.mean_diffusivity(tenfit.evals)
wm_mask = (np.logical_or(FA >= 0.4, (np.logical_and(FA >= 0.15, MD >= 0.0011))))
response = recursive_response(gtab, data, mask=wm_mask, sh_order=8,
peak_thr=0.01, init_fa=0.08,
init_trace=0.0021, iter=8, convergence=0.001,
parallel=True)
We can check the shape of the signal of the response function, which should be like a pancake:
response_signal = response.on_sphere(default_sphere)
# transform our data from 1D to 4D
response_signal = response_signal[None, None, None, :]
response_actor = actor.odf_slicer(response_signal, sphere=default_sphere,
colormap='plasma')
ren = window.Renderer()
ren.add(response_actor)
print('Saving illustration as csd_recursive_response.png')
window.record(ren, out_path='csd_recursive_response.png', size=(200, 200))
if interactive:
window.show(ren)
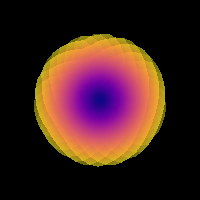
Estimated response function using recursive calibration.¶
ren.rm(response_actor)
## Step 2. fODF reconstruction
After estimating a response function for one of the strategies shown above, we are ready to start the deconvolution process. Let’s import the CSD model and fit the datasets.
from dipy.reconst.csdeconv import ConstrainedSphericalDeconvModel
csd_model = ConstrainedSphericalDeconvModel(gtab, response)
For illustration purposes we will fit only a small portion of the data.
data_small = data[20:50, 55:85, 38:39]
csd_fit = csd_model.fit(data_small)
Show the CSD-based ODFs also known as FODFs (fiber ODFs).
csd_odf = csd_fit.odf(default_sphere)
Here we visualize only a 30x30 region.
fodf_spheres = actor.odf_slicer(csd_odf, sphere=default_sphere, scale=0.9,
norm=False, colormap='plasma')
ren.add(fodf_spheres)
print('Saving illustration as csd_odfs.png')
window.record(ren, out_path='csd_odfs.png', size=(600, 600))
if interactive:
window.show(ren)
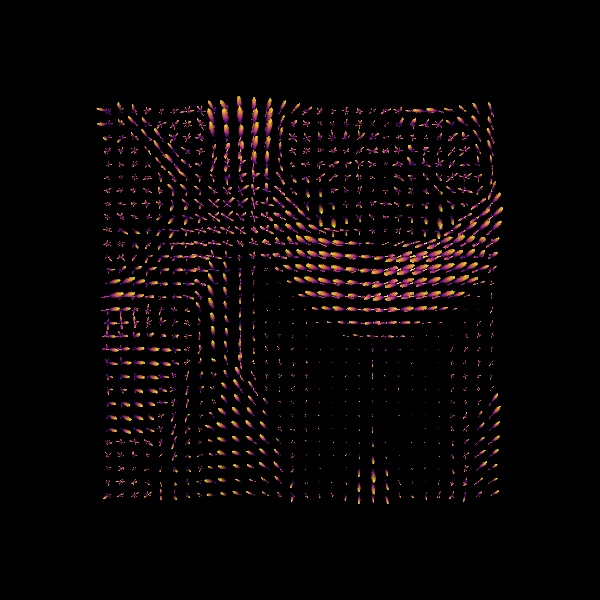
CSD ODFs.¶
In DIPY we also provide tools for finding the peak directions (maxima) of the
ODFs. For this purpose we recommend using peaks_from_model.
from dipy.direction import peaks_from_model
csd_peaks = peaks_from_model(model=csd_model,
data=data_small,
sphere=default_sphere,
relative_peak_threshold=.5,
min_separation_angle=25,
parallel=True)
window.clear(ren)
fodf_peaks = actor.peak_slicer(csd_peaks.peak_dirs, csd_peaks.peak_values)
ren.add(fodf_peaks)
print('Saving illustration as csd_peaks.png')
window.record(ren, out_path='csd_peaks.png', size=(600, 600))
if interactive:
window.show(ren)

CSD Peaks.¶
We can finally visualize both the ODFs and peaks in the same space.
fodf_spheres.GetProperty().SetOpacity(0.4)
ren.add(fodf_spheres)
print('Saving illustration as csd_both.png')
window.record(ren, out_path='csd_both.png', size=(600, 600))
if interactive:
window.show(ren)
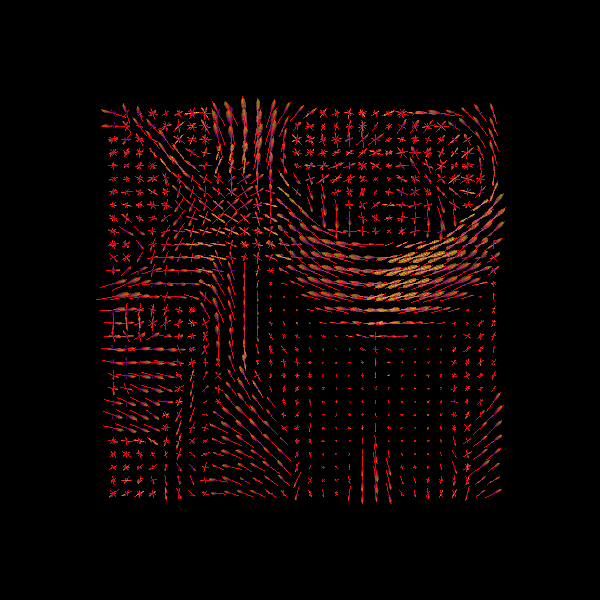
CSD Peaks and ODFs.¶
References¶
- Tournier2007
J-D. Tournier, F. Calamante and A. Connelly, “Robust determination of the fibre orientation distribution in diffusion MRI: Non-negativity constrained super-resolved spherical deconvolution”, Neuroimage, vol. 35, no. 4, pp. 1459-1472, 2007.
- Tax2014
C.M.W. Tax, B. Jeurissen, S.B. Vos, M.A. Viergever, A. Leemans, “Recursive calibration of the fiber response function for spherical deconvolution of diffusion MRI data”, Neuroimage, vol. 86, pp. 67-80, 2014.
Example source code
You can download the full source code of this example. This same script is also included in the dipy source distribution under the doc/examples/ directory.
