Diffeomorphic Registration with binary and fuzzy images¶
This example demonstrates registration of a binary and a fuzzy image. This could be seen as aligning a fuzzy (sensed) image to a binary (e.g., template) image.
import numpy as np
import matplotlib.pyplot as plt
from skimage import draw, filters
from dipy.align.imwarp import SymmetricDiffeomorphicRegistration
from dipy.align.metrics import SSDMetric
from dipy.viz import regtools
Let’s generate a sample template image as the combination of three ellipses. We will generate the fuzzy (sensed) version of the image by smoothing the reference image.
def draw_ellipse(img, center, axis):
rr, cc = draw.ellipse(center[0], center[1], axis[0], axis[1],
shape=img.shape)
img[rr, cc] = 1
return img
img_ref = np.zeros((64, 64))
img_ref = draw_ellipse(img_ref, (25, 15), (10, 5))
img_ref = draw_ellipse(img_ref, (20, 45), (15, 10))
img_ref = draw_ellipse(img_ref, (50, 40), (7, 15))
img_in = filters.gaussian(img_ref, sigma=3)
Let’s define a small visualization function.
def show_images(img_ref, img_warp, fig_name):
fig, axarr = plt.subplots(ncols=2, figsize=(12, 5))
axarr[0].set_title('warped image & reference contour')
axarr[0].imshow(img_warp)
axarr[0].contour(img_ref, colors='r')
ssd = np.sum((img_warp - img_ref) ** 2)
axarr[1].set_title('difference, SSD=%.02f' % ssd)
im = axarr[1].imshow(img_warp - img_ref)
plt.colorbar(im)
fig.tight_layout()
fig.savefig(fig_name + '.png')
show_images(img_ref, img_in, 'input')
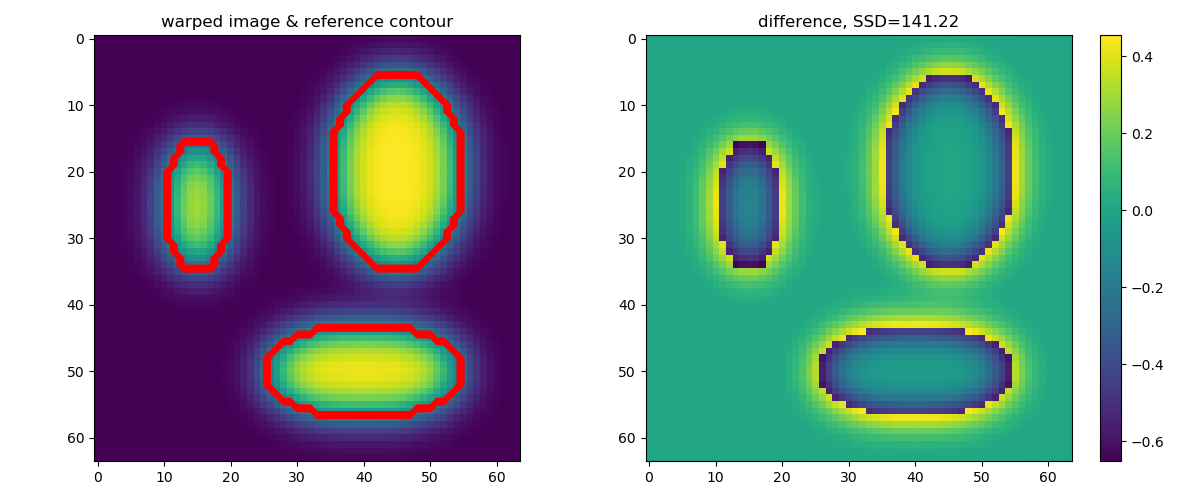
Input images before alignment.¶
Let’s the use the general Registration function with some naive parameters, such as set step_length as 1 assuming maximal step 1 pixel and reasonable small number of iteration since the deformation with already aligned images should be minimal.
sdr = SymmetricDiffeomorphicRegistration(metric=SSDMetric(img_ref.ndim),
step_length=1.0,
level_iters=[50, 100],
inv_iter=50,
ss_sigma_factor=0.1,
opt_tol=1.e-3)
Perform the registration with equal images.
mapping = sdr.optimize(img_ref.astype(float), img_ref.astype(float))
img_warp = mapping.transform(img_ref, 'linear')
show_images(img_ref, img_warp, 'output-0')
regtools.plot_2d_diffeomorphic_map(mapping, 5, 'map-0.png')
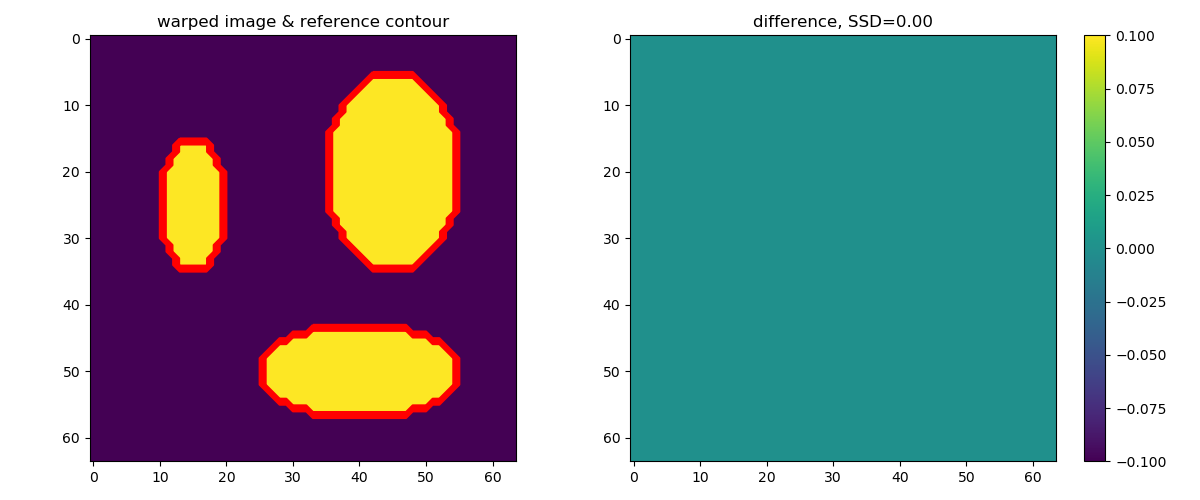
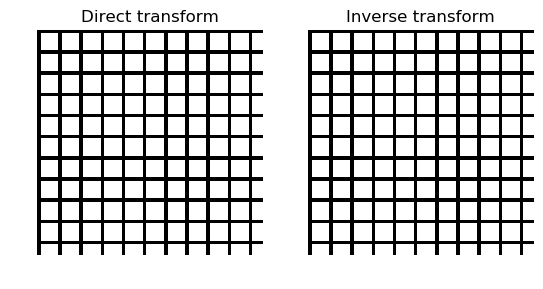
Registration results for default parameters and equal images.¶
Perform the registration with binary and fuzzy images.
mapping = sdr.optimize(img_ref.astype(float), img_in.astype(float))
img_warp = mapping.transform(img_in, 'linear')
show_images(img_ref, img_warp, 'output-1')
regtools.plot_2d_diffeomorphic_map(mapping, 5, 'map-1.png')
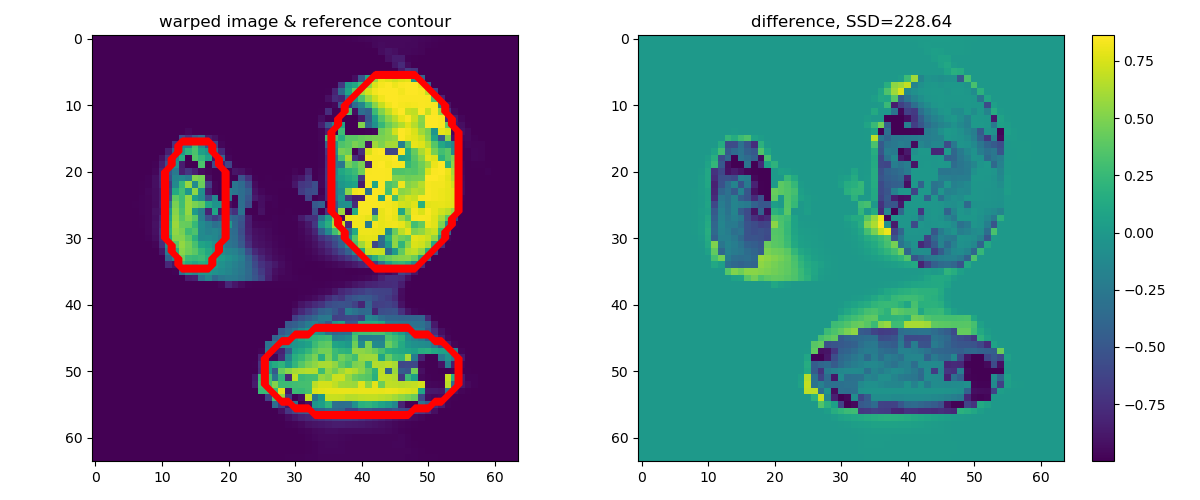
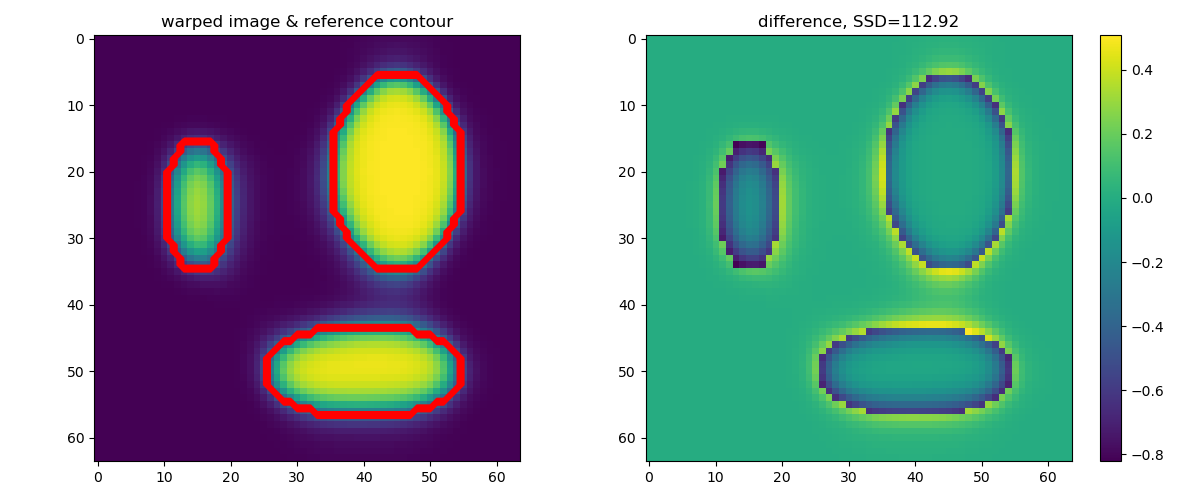
Registration results for a naive parameter configuration.¶
Note, we are still using multi-scale approach which makes step_length in the upper level multiplicatively larger. What happens if we set step_length to a rather small value?
sdr.step_length = 0.1
Perform the registration and examine the output.
mapping = sdr.optimize(img_ref.astype(float), img_in.astype(float))
img_warp = mapping.transform(img_in, 'linear')
show_images(img_ref, img_warp, 'output-2')
regtools.plot_2d_diffeomorphic_map(mapping, 5, 'map-2.png')
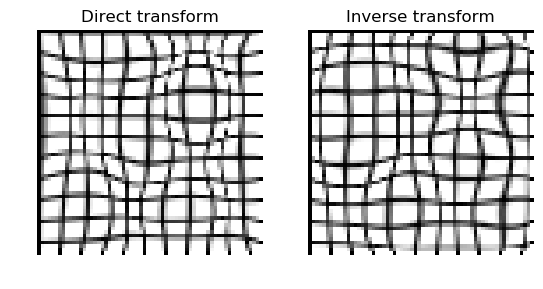
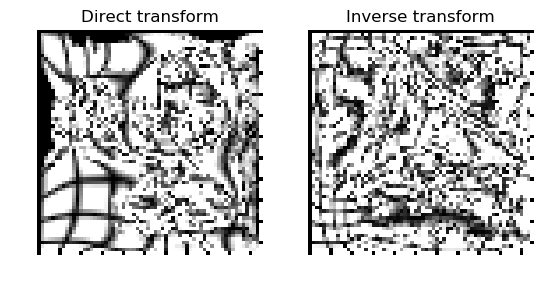
Registration results for decreased step size.¶
An alternative scenario is to use just a single scale level. Even though the warped image may look fine, the estimated deformations show that it is off the mark.
sdr = SymmetricDiffeomorphicRegistration(metric=SSDMetric(img_ref.ndim),
step_length=1.0,
level_iters=[100],
inv_iter=50,
ss_sigma_factor=0.1,
opt_tol=1.e-3)
Perform the registration.
mapping = sdr.optimize(img_ref.astype(float), img_in.astype(float))
img_warp = mapping.transform(img_in, 'linear')
show_images(img_ref, img_warp, 'output-3')
regtools.plot_2d_diffeomorphic_map(mapping, 5, 'map-3.png')
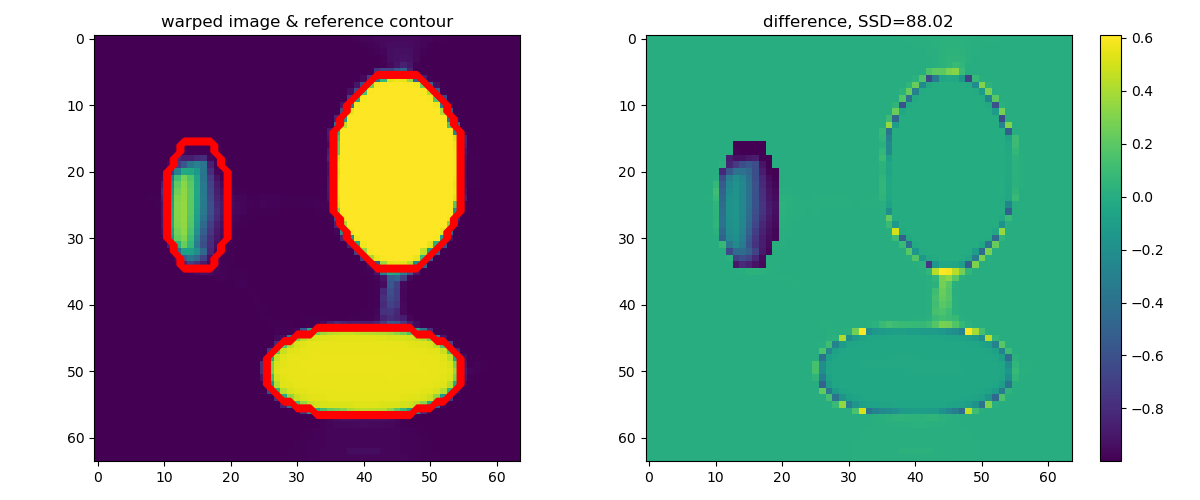
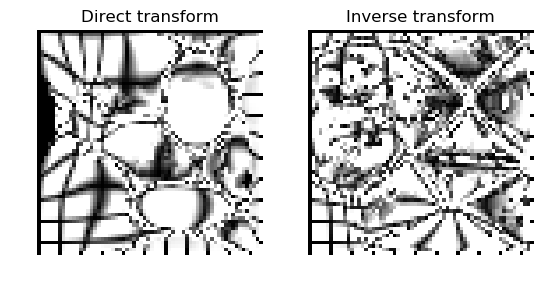
Registration results for single level.¶
Example source code
You can download the full source code of this example. This same script is also included in the dipy source distribution under the doc/examples/ directory.
