Gradients and Spheres¶
This example shows how you can create gradient tables and sphere objects using DIPY.
Usually, as we saw in Getting started with DIPY, you load your b-values and b-vectors from disk and then you can create your own gradient table. But this time let’s say that you are an MR physicist and you want to design a new gradient scheme or you are a scientist who wants to simulate many different gradient schemes.
Now let’s assume that you are interested in creating a multi-shell acquisition with 2-shells, one at b=1000 \(s/mm^2\) and one at b=2500 \(s/mm^2\). For both shells let’s say that we want a specific number of gradients (64) and we want to have the points on the sphere evenly distributed.
This is possible using the disperse_charges which is an implementation of
electrostatic repulsion [Jones1999].
import numpy as np
from dipy.core.sphere import disperse_charges, Sphere, HemiSphere
We can first create some random points on a HemiSphere using spherical polar
coordinates.
n_pts = 64
theta = np.pi * np.random.rand(n_pts)
phi = 2 * np.pi * np.random.rand(n_pts)
hsph_initial = HemiSphere(theta=theta, phi=phi)
Next, we call disperse_charges which will iteratively move the points so that
the electrostatic potential energy is minimized.
hsph_updated, potential = disperse_charges(hsph_initial, 5000)
In hsph_updated we have the updated HemiSphere with the points nicely
distributed on the hemisphere. Let’s visualize them.
from dipy.viz import window, actor
# Enables/disables interactive visualization
interactive = False
ren = window.Renderer()
ren.SetBackground(1, 1, 1)
ren.add(actor.point(hsph_initial.vertices, window.colors.red,
point_radius=0.05))
ren.add(actor.point(hsph_updated.vertices, window.colors.green,
point_radius=0.05))
print('Saving illustration as initial_vs_updated.png')
window.record(ren, out_path='initial_vs_updated.png', size=(300, 300))
if interactive:
window.show(ren)
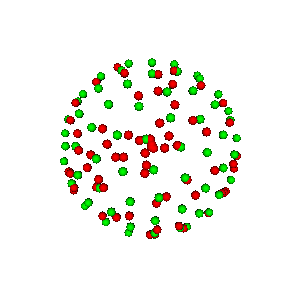
Illustration of electrostatic repulsion of red points which become green points.¶
We can also create a sphere from the hemisphere and show it in the following way.
sph = Sphere(xyz=np.vstack((hsph_updated.vertices, -hsph_updated.vertices)))
window.rm_all(ren)
ren.add(actor.point(sph.vertices, window.colors.green, point_radius=0.05))
print('Saving illustration as full_sphere.png')
window.record(ren, out_path='full_sphere.png', size=(300, 300))
if interactive:
window.show(ren)
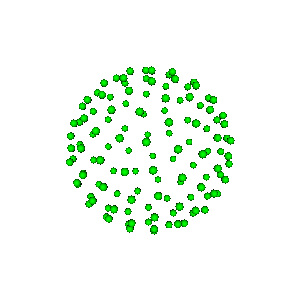
Full sphere.¶
It is time to create the Gradients. For this purpose we will use the
function gradient_table and fill it with the hsph_updated vectors that
we created above.
from dipy.core.gradients import gradient_table
vertices = hsph_updated.vertices
values = np.ones(vertices.shape[0])
We need two stacks of vertices, one for every shell, and we need two sets
of b-values, one at 1000 \(s/mm^2\), and one at 2500 \(s/mm^2\), as we discussed
previously.
bvecs = np.vstack((vertices, vertices))
bvals = np.hstack((1000 * values, 2500 * values))
We can also add some b0s. Let’s add one at the beginning and one at the end.
bvecs = np.insert(bvecs, (0, bvecs.shape[0]), np.array([0, 0, 0]), axis=0)
bvals = np.insert(bvals, (0, bvals.shape[0]), 0)
print(bvals)
[ 0. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000.
1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000.
1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000.
1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000.
1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000.
1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000.
1000. 1000. 1000. 1000. 1000. 2500. 2500. 2500. 2500. 2500.
2500. 2500. 2500. 2500. 2500. 2500. 2500. 2500. 2500. 2500.
2500. 2500. 2500. 2500. 2500. 2500. 2500. 2500. 2500. 2500.
2500. 2500. 2500. 2500. 2500. 2500. 2500. 2500. 2500. 2500.
2500. 2500. 2500. 2500. 2500. 2500. 2500. 2500. 2500. 2500.
2500. 2500. 2500. 2500. 2500. 2500. 2500. 2500. 2500. 2500.
2500. 2500. 2500. 2500. 2500. 2500. 2500. 2500. 2500. 0.]
print(bvecs)
[[ 0. 0. 0. ]
[-0.80451777 -0.16877559 0.56944355]
[ 0.32822557 -0.94355999 0.04430036]
[-0.23584135 -0.96241331 0.13468285]
[-0.39207424 -0.73505312 0.55314981]
[-0.32539386 -0.16751384 0.93062235]
[-0.82043195 -0.39411534 0.41420347]
[ 0.65741493 0.74947875 0.07802061]
[ 0.88853765 0.45303621 0.07251925]
[ 0.39638642 -0.15185138 0.90543855]
...
[ 0.10175269 0.08197111 0.99142681]
[ 0.50577702 -0.37862345 0.77513476]
[ 0.42845026 0.40155296 0.80943535]
[ 0.26939707 0.81103868 0.51927014]
[-0.48938584 -0.43780086 0.75420946]
[ 0. 0. 0. ]]
Both b-values and b-vectors look correct. Let’s now create the
GradientTable.
gtab = gradient_table(bvals, bvecs)
window.rm_all(ren)
We can also visualize the gradients. Let’s color the first shell blue and the second shell cyan.
colors_b1000 = window.colors.blue * np.ones(vertices.shape)
colors_b2500 = window.colors.cyan * np.ones(vertices.shape)
colors = np.vstack((colors_b1000, colors_b2500))
colors = np.insert(colors, (0, colors.shape[0]), np.array([0, 0, 0]), axis=0)
colors = np.ascontiguousarray(colors)
ren.add(actor.point(gtab.gradients, colors, point_radius=100))
print('Saving illustration as gradients.png')
window.record(ren, out_path='gradients.png', size=(300, 300))
if interactive:
window.show(ren)

Diffusion gradients.¶
References¶
- Jones1999
Jones, DK. et al. Optimal strategies for measuring diffusion in anisotropic systems by magnetic resonance imaging, Magnetic Resonance in Medicine, vol 42, no 3, 515-525, 1999.
Example source code
You can download the full source code of this example. This same script is also included in the dipy source distribution under the doc/examples/ directory.
