Note
Go to the end to download the full example code
Reconstruction of the diffusion signal with the kurtosis tensor model#
The diffusion kurtosis model is an expansion of the diffusion tensor model (see Reconstruction of the diffusion signal with the Tensor model). In addition to the diffusion tensor (DT), the diffusion kurtosis model quantifies the degree to which water diffusion in biological tissues is non-Gaussian using the kurtosis tensor (KT) [Jensen2005].
Measurements of non-Gaussian diffusion from the diffusion kurtosis model are of interest because they can be used to characterize tissue microstructural heterogeneity [Jensen2010]. Moreover, DKI can be used to: 1) derive concrete biophysical parameters, such as the density of axonal fibers and diffusion tortuosity [Fierem2011] (see Reconstruction of the diffusion signal with the WMTI model); and 2) resolve crossing fibers in tractography and to obtain invariant rotational measures not limited to well-aligned fiber populations [NetoHe2015].
The diffusion kurtosis model expresses the diffusion-weighted signal as:
where \(\mathbf{b}\) is the applied diffusion weighting (which is dependent on the measurement parameters), \(S_0\) is the signal in the absence of diffusion gradient sensitization, \(\mathbf{D(n)}\) is the value of diffusion along direction \(\mathbf{n}\), and \(\mathbf{K(n)}\) is the value of kurtosis along direction \(\mathbf{n}\). The directional diffusion \(\mathbf{D(n)}\) and kurtosis \(\mathbf{K(n)}\) can be related to the diffusion tensor (DT) and kurtosis tensor (KT) using the following equations:
and
where \(D_{ij}\) are the elements of the second-order DT, and \(W_{ijkl}\) the elements of the fourth-order KT and \(MD\) is the mean diffusivity. As the DT, KT has antipodal symmetry and thus only 15 Wijkl elements are needed to fully characterize the KT:
In the following example we show how to fit the diffusion kurtosis model on diffusion-weighted multi-shell datasets and how to estimate diffusion kurtosis based statistics.
First, we import all relevant modules:
import numpy as np
import dipy.reconst.dki as dki
import dipy.reconst.dti as dti
from dipy.core.gradients import gradient_table
from dipy.data import get_fnames
from dipy.io.gradients import read_bvals_bvecs
from dipy.io.image import load_nifti
from dipy.segment.mask import median_otsu
from dipy.viz.plotting import compare_maps
from scipy.ndimage import gaussian_filter
DKI requires multi-shell data, i.e. data acquired from more than one non-zero b-value. Here, we use fetch to download a multi-shell dataset which was kindly provided by Hansen and Jespersen (more details about the data are provided in their paper [Hansen2016]). The total size of the downloaded data is 192 MBytes, however you only need to fetch it once.
fraw, fbval, fbvec, t1_fname = get_fnames('cfin_multib')
data, affine = load_nifti(fraw)
bvals, bvecs = read_bvals_bvecs(fbval, fbvec)
gtab = gradient_table(bvals, bvecs)
Function get_fnames downloads and outputs the paths of the data,
load_nifti returns the data as a nibabel Nifti1Image object, and
read_bvals_bvecs loads the arrays containing the information about the
b-values and b-vectors. These later arrays are converted to the
GradientTable object required for Dipy’s data reconstruction.
Before fitting the data, we perform some data pre-processing. We first compute a brain mask to avoid unnecessary calculations on the background of the image.
maskdata, mask = median_otsu(data, vol_idx=[0, 1], median_radius=4, numpass=2,
autocrop=False, dilate=1)
Since the diffusion kurtosis models involves the estimation of a large number of parameters [TaxCMW2015] and since the non-Gaussian components of the diffusion signal are more sensitive to artefacts [NetoHe2012], it might be favorable to suppress the effects of noise and artefacts before diffusion kurtosis fitting. In this example the effects of noise and artefacts are suppress by using 3D Gaussian smoothing (with a Gaussian kernel with fwhm=1.25) as suggested by pioneer DKI studies (e.g. [Jensen2005], [NetoHe2012]). Although here the Gaussian smoothing is used so that results are comparable to these studies, it is important to note that more advanced noise and artifact suppression algorithms are available in DIPY, e.g. the Marcenko-Pastur PCA denoising algorithm (Denoise images using the Marcenko-Pastur PCA algorithm) and the Gibbs artefact suppression algorithm (Suppress Gibbs oscillations).
fwhm = 1.25
gauss_std = fwhm / np.sqrt(8 * np.log(2)) # converting fwhm to Gaussian std
data_smooth = np.zeros(data.shape)
for v in range(data.shape[-1]):
data_smooth[..., v] = gaussian_filter(data[..., v], sigma=gauss_std)
Now that we have loaded and pre-processed the data we can go forward with DKI fitting. For this, the DKI model is first defined for the data’s GradientTable object by instantiating the DiffusionKurtosisModel object in the following way:
dkimodel = dki.DiffusionKurtosisModel(gtab)
To fit the data using the defined model object, we call the fit function
of this object. For the purpose of this example, we will only fit a
single slice of the data:
data_smooth = data_smooth[:, :, 9:10]
mask = mask[:, :, 9:10]
dkifit = dkimodel.fit(data_smooth, mask=mask)
0%| | 0/3121 [00:00<?, ?it/s]
2%|██▎ | 64/3121 [00:00<00:04, 637.81it/s]
5%|█████▍ | 149/3121 [00:00<00:03, 753.95it/s]
7%|████████▌ | 234/3121 [00:00<00:03, 794.00it/s]
10%|███████████▍ | 314/3121 [00:00<00:03, 793.35it/s]
13%|██████████████▍ | 394/3121 [00:00<00:03, 793.91it/s]
16%|█████████████████▋ | 484/3121 [00:00<00:03, 827.53it/s]
18%|████████████████████▉ | 572/3121 [00:00<00:03, 842.55it/s]
21%|███████████████████████▉ | 657/3121 [00:00<00:02, 842.51it/s]
24%|███████████████████████████ | 742/3121 [00:00<00:02, 842.22it/s]
26%|██████████████████████████████▏ | 827/3121 [00:01<00:02, 841.78it/s]
29%|█████████████████████████████████▎ | 912/3121 [00:01<00:02, 840.69it/s]
32%|████████████████████████████████████▍ | 1006/3121 [00:01<00:02, 868.77it/s]
35%|███████████████████████████████████████▉ | 1103/3121 [00:01<00:02, 896.71it/s]
38%|███████████████████████████████████████████▏ | 1193/3121 [00:01<00:02, 894.68it/s]
41%|██████████████████████████████████████████████▍ | 1283/3121 [00:01<00:02, 853.43it/s]
44%|█████████████████████████████████████████████████▉ | 1379/3121 [00:01<00:01, 876.93it/s]
47%|█████████████████████████████████████████████████████▏ | 1468/3121 [00:01<00:01, 857.35it/s]
50%|████████████████████████████████████████████████████████▌ | 1562/3121 [00:01<00:01, 874.25it/s]
53%|███████████████████████████████████████████████████████████▋ | 1650/3121 [00:01<00:01, 848.79it/s]
57%|███████████████████████████████████████████████████████████████▉ | 1767/3121 [00:02<00:01, 937.24it/s]
60%|████████████████████████████████████████████████████████████████████▏ | 1883/3121 [00:02<00:01, 998.33it/s]
64%|███████████████████████████████████████████████████████████████████████▊ | 1984/3121 [00:02<00:01, 998.96it/s]
67%|███████████████████████████████████████████████████████████████████████████▍ | 2085/3121 [00:02<00:01, 965.04it/s]
70%|███████████████████████████████████████████████████████████████████████████████ | 2182/3121 [00:02<00:00, 963.94it/s]
73%|██████████████████████████████████████████████████████████████████████████████████▌ | 2279/3121 [00:02<00:00, 935.83it/s]
76%|█████████████████████████████████████████████████████████████████████████████████████▉ | 2375/3121 [00:02<00:00, 940.64it/s]
79%|█████████████████████████████████████████████████████████████████████████████████████████▍ | 2470/3121 [00:02<00:00, 919.46it/s]
82%|█████████████████████████████████████████████████████████████████████████████████████████████▏ | 2573/3121 [00:02<00:00, 948.46it/s]
86%|████████████████████████████████████████████████████████████████████████████████████████████████▋ | 2693/3121 [00:02<00:00, 1018.39it/s]
90%|████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 2802/3121 [00:03<00:00, 1034.88it/s]
93%|████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 2906/3121 [00:03<00:00, 1027.82it/s]
97%|████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 3015/3121 [00:03<00:00, 1043.00it/s]
100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████▉| 3120/3121 [00:03<00:00, 1012.75it/s]
100%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 3121/3121 [00:03<00:00, 912.33it/s]
The fit method creates a DiffusionKurtosisFit object, which contains all the
diffusion and kurtosis fitting parameters and other DKI attributes. For
instance, since the diffusion kurtosis model estimates the diffusion tensor,
all standard diffusion tensor statistics can be computed from the
DiffusionKurtosisFit instance. For example, we can extract the fractional
anisotropy (FA), the mean diffusivity (MD), the axial diffusivity (AD) and
the radial diffusivity (RD) from the DiffusionKurtosisiFit instance. Of
course, these measures can also be computed from DIPY’s TensorModel fit,
and should be analogous; however, theoretically, the diffusion statistics
from the kurtosis model are expected to have better accuracy, since DKI’s
diffusion tensor are decoupled from higher order terms effects
[Veraar2011], [NetoHe2012]. Below we compare the FA, MD, AD, and RD,
computed from both DTI and DKI.
tenmodel = dti.TensorModel(gtab)
tenfit = tenmodel.fit(data_smooth, mask=mask)
fits = [tenfit, dkifit]
maps = ['fa', 'md', 'ad', 'rd']
fit_labels = ['DTI', 'DKI']
map_kwargs = [{'vmax': 0.7}, {'vmax': 2e-3}, {'vmax': 2e-3}, {'vmax': 2e-3}]
compare_maps(fits, maps, fit_labels=fit_labels, map_kwargs=map_kwargs,
filename='Diffusion_tensor_measures_from_DTI_and_DKI.png')
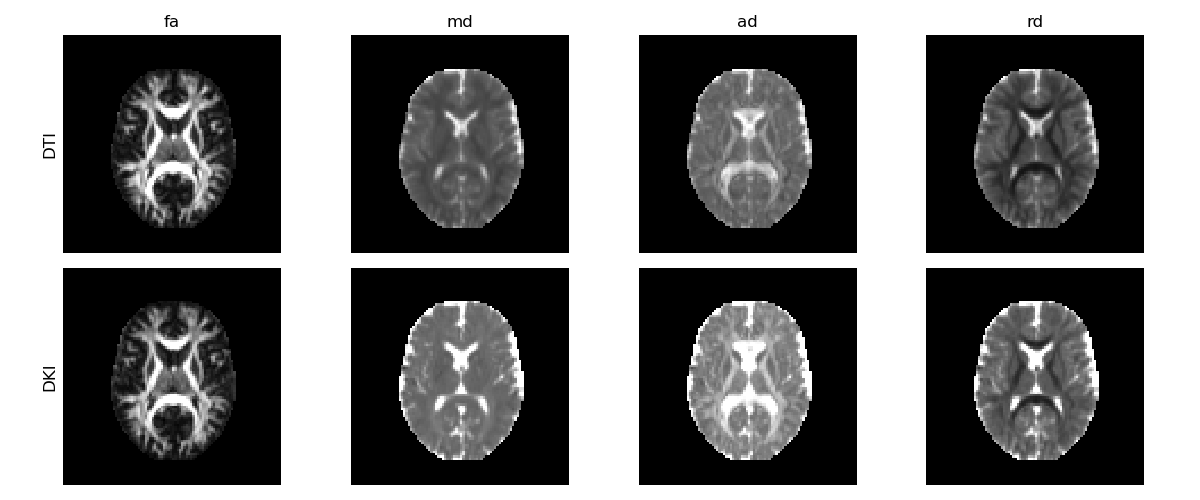
Diffusion tensor measures obtained from the diffusion tensor estimated from DKI (upper panels) and DTI (lower panels).
DTI’s diffusion estimates present lower values than DKI’s estimates, showing that DTI’s diffusion measurements are underestimated by higher order effects.
In addition to the standard diffusion statistics, the DiffusionKurtosisFit instance can be used to estimate the non-Gaussian measures of mean kurtosis (MK), the axial kurtosis (AK) and the radial kurtosis (RK).
maps = ['mk', 'ak', 'rk']
compare_maps([dkifit], maps, fit_labels=['DKI'],
map_kwargs={'vmin': 0, 'vmax': 1.5},
filename='Kurtosis_tensor_standard_measures.png')
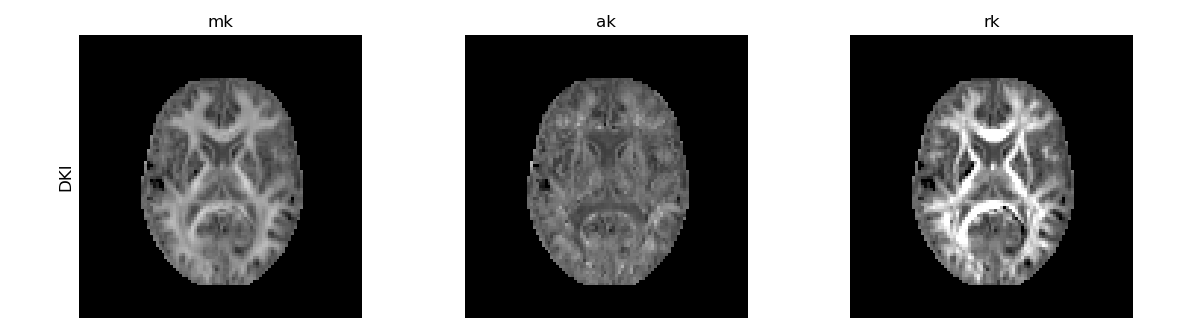
DKI standard kurtosis measures.
The non-Gaussian behaviour of the diffusion signal is expected to be higher when tissue water is confined by multiple compartments. MK is, therefore, higher in white matter since it is highly compartmentalized by myelin sheaths. These water diffusion compartmentalization is expected to be more pronounced perpendicularly to white matter fibers and thus the RK map presents higher amplitudes than the AK map.
It is important to note that kurtosis estimates might present negative estimates in deep white matter regions (e.g. the band of dark voxels in the RK map above). These negative kurtosis values are artefactual and might be induced by: 1) low radial diffusivities of aligned white matter - since it is very hard to capture non-Gaussian information in radial direction due to it’s low diffusion decays, radial kurtosis estimates (and consequently the mean kurtosis estimates) might have low robustness and tendency to exhibit negative values [NetoHe2012]; 2) Gibbs artefacts - MRI images might be corrupted by signal oscillation artefact between tissue’s edges if an inadequate number of high frequencies of the k-space is sampled. These oscillations might have different signs on images acquired with different diffusion-weighted and inducing negative biases in kurtosis parametric maps [Perron2015], [NetoHe2018].
One can try to suppress this issue by using the more advance noise and artefact suppression algorithms, e.g., as mentioned above, the MP-PCA denoising (Denoise images using the Marcenko-Pastur PCA algorithm) and Gibbs Unringing (Suppress Gibbs oscillations) algorithms. Alternatively, one can overcome this artefact by computing the kurtosis values from powder-averaged diffusion-weighted signals. The details on how to compute the kurtosis from powder-average signals in dipy are described in follow the tutorial (Mean signal diffusion kurtosis imaging (MSDKI)). Finally, one can use constrained optimization to ensure that the fitted parameters are physically plausible [DelaHa2020], as we will illustrate in the next section. Ideally though, artefacts such as Gibbs ringing should be corrected for as well as possible before using constrained optimization.
Constrained optimization for DKI#
When instantiating the DiffusionKurtosisModel, the model can be set up to use
constraints with the option fit_method=’CLS’ (for ordinary least squares)
or with fit_method=’CWLS’ (for weighted least squares). Constrained fitting
takes more time than unconstrained fitting, but is generally recommended to
prevent physically unplausible parameter estimates [DelaHa2020]. For
performance purposes it is recommended to use the MOSEK solver
(https://www.mosek.com/) by setting cvxpy_solver='MOSEK'. Different
solvers can differ greatly in terms of runtime and solution accuracy, and in
some cases solvers may show warnings about convergence or recommended option
settings.
Note
In certain atypical scenarios, the DKI+ constraints could potentially be too restrictive. Always check the results of a constrained fit with their unconstrained counterpart to verify that there are no unexpected qualitative differences.
dkimodel_plus = dki.DiffusionKurtosisModel(gtab, fit_method='CLS')
dkifit_plus = dkimodel_plus.fit(data_smooth, mask=mask)
0%| | 0/3121 [00:00<?, ?it/s]
0%| | 1/3121 [00:00<11:51, 4.39it/s]
0%|▌ | 15/3121 [00:00<00:55, 56.09it/s]
1%|█▏ | 32/3121 [00:00<00:32, 95.82it/s]
2%|█▋ | 47/3121 [00:00<00:27, 113.38it/s]
2%|██▎ | 62/3121 [00:00<00:24, 124.88it/s]
3%|██▉ | 80/3121 [00:00<00:21, 139.19it/s]
3%|███▌ | 97/3121 [00:00<00:20, 146.41it/s]
4%|████▏ | 113/3121 [00:00<00:20, 150.07it/s]
4%|████▋ | 130/3121 [00:01<00:19, 155.68it/s]
5%|█████▎ | 146/3121 [00:01<00:19, 156.55it/s]
5%|█████▉ | 164/3121 [00:01<00:18, 163.28it/s]
6%|██████▊ | 186/3121 [00:01<00:16, 179.86it/s]
7%|███████▍ | 205/3121 [00:01<00:16, 177.12it/s]
7%|████████▏ | 223/3121 [00:01<00:17, 167.74it/s]
8%|████████▊ | 240/3121 [00:01<00:17, 168.08it/s]
8%|█████████▍ | 258/3121 [00:01<00:16, 171.17it/s]
9%|██████████ | 276/3121 [00:01<00:17, 160.33it/s]
9%|██████████▋ | 293/3121 [00:02<00:17, 157.47it/s]
10%|███████████▎ | 309/3121 [00:02<00:18, 153.64it/s]
10%|███████████▊ | 325/3121 [00:02<00:18, 155.10it/s]
11%|████████████▍ | 342/3121 [00:02<00:17, 158.99it/s]
12%|█████████████▏ | 361/3121 [00:02<00:16, 167.48it/s]
12%|█████████████▉ | 383/3121 [00:02<00:15, 182.32it/s]
13%|██████████████▋ | 403/3121 [00:02<00:14, 187.10it/s]
14%|███████████████▍ | 422/3121 [00:02<00:14, 182.05it/s]
14%|████████████████ | 441/3121 [00:02<00:14, 183.92it/s]
15%|████████████████▊ | 460/3121 [00:02<00:15, 174.82it/s]
15%|█████████████████▍ | 478/3121 [00:03<00:15, 175.85it/s]
16%|██████████████████ | 496/3121 [00:03<00:15, 171.66it/s]
16%|██████████████████▊ | 514/3121 [00:03<00:15, 173.76it/s]
17%|███████████████████▌ | 534/3121 [00:03<00:14, 180.88it/s]
18%|████████████████████▏ | 554/3121 [00:03<00:13, 185.95it/s]
18%|████████████████████▉ | 573/3121 [00:03<00:14, 173.27it/s]
19%|█████████████████████▌ | 591/3121 [00:03<00:15, 162.45it/s]
19%|██████████████████████▏ | 608/3121 [00:03<00:16, 150.56it/s]
20%|██████████████████████▊ | 624/3121 [00:03<00:16, 151.85it/s]
21%|███████████████████████▍ | 643/3121 [00:04<00:15, 161.91it/s]
21%|████████████████████████▏ | 663/3121 [00:04<00:14, 172.17it/s]
22%|████████████████████████▊ | 681/3121 [00:04<00:14, 169.21it/s]
22%|█████████████████████████▌ | 699/3121 [00:04<00:14, 171.87it/s]
23%|██████████████████████████▏ | 717/3121 [00:04<00:13, 173.48it/s]
24%|██████████████████████████▊ | 735/3121 [00:04<00:14, 170.00it/s]
24%|███████████████████████████▌ | 753/3121 [00:04<00:14, 159.64it/s]
25%|████████████████████████████▏ | 770/3121 [00:04<00:15, 153.73it/s]
25%|████████████████████████████▋ | 786/3121 [00:04<00:15, 155.15it/s]
26%|█████████████████████████████▋ | 812/3121 [00:05<00:12, 183.63it/s]
27%|██████████████████████████████▍ | 833/3121 [00:05<00:12, 189.65it/s]
27%|███████████████████████████████▏ | 855/3121 [00:05<00:11, 197.95it/s]
28%|████████████████████████████████ | 878/3121 [00:05<00:10, 206.73it/s]
29%|████████████████████████████████▊ | 899/3121 [00:05<00:11, 201.22it/s]
29%|█████████████████████████████████▌ | 920/3121 [00:05<00:11, 198.75it/s]
30%|██████████████████████████████████▍ | 942/3121 [00:05<00:10, 203.17it/s]
31%|███████████████████████████████████▏ | 963/3121 [00:05<00:11, 193.58it/s]
31%|███████████████████████████████████▉ | 983/3121 [00:05<00:11, 184.63it/s]
32%|████████████████████████████████████▎ | 1002/3121 [00:06<00:12, 172.21it/s]
33%|█████████████████████████████████████ | 1024/3121 [00:06<00:11, 183.54it/s]
33%|█████████████████████████████████████▊ | 1043/3121 [00:06<00:11, 180.04it/s]
34%|██████████████████████████████████████▋ | 1067/3121 [00:06<00:10, 196.19it/s]
35%|███████████████████████████████████████▎ | 1087/3121 [00:06<00:10, 186.10it/s]
35%|████████████████████████████████████████ | 1106/3121 [00:06<00:10, 186.72it/s]
36%|████████████████████████████████████████▋ | 1125/3121 [00:06<00:11, 174.34it/s]
37%|█████████████████████████████████████████▍ | 1143/3121 [00:06<00:12, 160.57it/s]
37%|██████████████████████████████████████████ | 1162/3121 [00:06<00:11, 167.96it/s]
38%|██████████████████████████████████████████▋ | 1180/3121 [00:07<00:12, 154.02it/s]
38%|███████████████████████████████████████████▎ | 1196/3121 [00:07<00:12, 155.21it/s]
39%|███████████████████████████████████████████▉ | 1213/3121 [00:07<00:12, 158.80it/s]
39%|████████████████████████████████████████████▌ | 1232/3121 [00:07<00:11, 165.07it/s]
40%|█████████████████████████████████████████████▍ | 1256/3121 [00:07<00:10, 182.69it/s]
41%|██████████████████████████████████████████████▎ | 1278/3121 [00:07<00:09, 192.74it/s]
42%|██████████████████████████████████████████████▉ | 1298/3121 [00:07<00:09, 192.50it/s]
42%|███████████████████████████████████████████████▊ | 1322/3121 [00:07<00:08, 203.54it/s]
43%|████████████████████████████████████████████████▋ | 1344/3121 [00:07<00:08, 206.67it/s]
44%|█████████████████████████████████████████████████▍ | 1365/3121 [00:08<00:09, 191.41it/s]
44%|██████████████████████████████████████████████████▏ | 1385/3121 [00:08<00:09, 182.23it/s]
45%|██████████████████████████████████████████████████▉ | 1406/3121 [00:08<00:09, 189.46it/s]
46%|███████████████████████████████████████████████████▋ | 1426/3121 [00:08<00:09, 186.70it/s]
46%|████████████████████████████████████████████████████▎ | 1445/3121 [00:08<00:09, 173.46it/s]
47%|█████████████████████████████████████████████████████ | 1465/3121 [00:08<00:09, 179.15it/s]
48%|█████████████████████████████████████████████████████▋ | 1484/3121 [00:08<00:09, 173.03it/s]
48%|██████████████████████████████████████████████████████▍ | 1502/3121 [00:08<00:09, 173.50it/s]
49%|███████████████████████████████████████████████████████ | 1520/3121 [00:08<00:09, 170.07it/s]
49%|███████████████████████████████████████████████████████▋ | 1538/3121 [00:09<00:09, 167.54it/s]
50%|████████████████████████████████████████████████████████▎ | 1555/3121 [00:09<00:09, 158.88it/s]
50%|████████████████████████████████████████████████████████▉ | 1571/3121 [00:09<00:10, 150.53it/s]
51%|█████████████████████████████████████████████████████████▍ | 1587/3121 [00:09<00:10, 148.63it/s]
52%|██████████████████████████████████████████████████████████▎ | 1611/3121 [00:09<00:08, 173.11it/s]
52%|██████████████████████████████████████████████████████████▉ | 1629/3121 [00:09<00:08, 174.51it/s]
53%|███████████████████████████████████████████████████████████▋ | 1648/3121 [00:09<00:08, 174.37it/s]
53%|████████████████████████████████████████████████████████████▎ | 1666/3121 [00:09<00:08, 169.75it/s]
54%|████████████████████████████████████████████████████████████▉ | 1684/3121 [00:09<00:09, 154.79it/s]
55%|█████████████████████████████████████████████████████████████▌ | 1701/3121 [00:10<00:08, 158.54it/s]
55%|██████████████████████████████████████████████████████████████▍ | 1724/3121 [00:10<00:07, 177.72it/s]
56%|███████████████████████████████████████████████████████████████▏ | 1746/3121 [00:10<00:07, 189.11it/s]
57%|████████████████████████████████████████████████████████████████ | 1771/3121 [00:10<00:06, 206.02it/s]
58%|█████████████████████████████████████████████████████████████████ | 1797/3121 [00:10<00:05, 221.03it/s]
58%|██████████████████████████████████████████████████████████████████ | 1824/3121 [00:10<00:05, 234.58it/s]
59%|██████████████████████████████████████████████████████████████████▉ | 1848/3121 [00:10<00:05, 235.43it/s]
60%|███████████████████████████████████████████████████████████████████▊ | 1872/3121 [00:10<00:05, 222.92it/s]
61%|████████████████████████████████████████████████████████████████████▌ | 1895/3121 [00:10<00:06, 202.45it/s]
61%|█████████████████████████████████████████████████████████████████████▎ | 1916/3121 [00:11<00:06, 187.63it/s]
62%|██████████████████████████████████████████████████████████████████████ | 1936/3121 [00:11<00:06, 172.44it/s]
63%|██████████████████████████████████████████████████████████████████████▋ | 1954/3121 [00:11<00:07, 166.34it/s]
63%|███████████████████████████████████████████████████████████████████████▎ | 1971/3121 [00:11<00:06, 166.07it/s]
64%|████████████████████████████████████████████████████████████████████████ | 1990/3121 [00:11<00:06, 171.98it/s]
64%|████████████████████████████████████████████████████████████████████████▊ | 2010/3121 [00:11<00:06, 179.25it/s]
65%|█████████████████████████████████████████████████████████████████████████▍ | 2029/3121 [00:11<00:06, 164.72it/s]
66%|██████████████████████████████████████████████████████████████████████████ | 2046/3121 [00:11<00:06, 165.27it/s]
66%|██████████████████████████████████████████████████████████████████████████▊ | 2065/3121 [00:11<00:06, 170.78it/s]
67%|███████████████████████████████████████████████████████████████████████████▍ | 2083/3121 [00:12<00:06, 163.90it/s]
67%|████████████████████████████████████████████████████████████████████████████ | 2100/3121 [00:12<00:06, 152.62it/s]
68%|████████████████████████████████████████████████████████████████████████████▊ | 2120/3121 [00:12<00:06, 164.79it/s]
69%|█████████████████████████████████████████████████████████████████████████████▍ | 2140/3121 [00:12<00:05, 174.06it/s]
69%|██████████████████████████████████████████████████████████████████████████████▏ | 2158/3121 [00:12<00:05, 170.47it/s]
70%|██████████████████████████████████████████████████████████████████████████████▊ | 2176/3121 [00:12<00:05, 168.02it/s]
70%|███████████████████████████████████████████████████████████████████████████████▌ | 2196/3121 [00:12<00:05, 176.49it/s]
71%|████████████████████████████████████████████████████████████████████████████████▎ | 2217/3121 [00:12<00:04, 185.65it/s]
72%|█████████████████████████████████████████████████████████████████████████████████▏ | 2243/3121 [00:12<00:04, 206.54it/s]
73%|█████████████████████████████████████████████████████████████████████████████████▉ | 2264/3121 [00:13<00:04, 185.07it/s]
73%|██████████████████████████████████████████████████████████████████████████████████▋ | 2284/3121 [00:13<00:04, 170.10it/s]
74%|███████████████████████████████████████████████████████████████████████████████████▎ | 2302/3121 [00:13<00:04, 172.28it/s]
74%|███████████████████████████████████████████████████████████████████████████████████▉ | 2320/3121 [00:13<00:04, 169.37it/s]
75%|████████████████████████████████████████████████████████████████████████████████████▋ | 2338/3121 [00:13<00:04, 159.68it/s]
75%|█████████████████████████████████████████████████████████████████████████████████████▎ | 2356/3121 [00:13<00:04, 163.76it/s]
76%|█████████████████████████████████████████████████████████████████████████████████████▉ | 2375/3121 [00:13<00:04, 170.53it/s]
77%|██████████████████████████████████████████████████████████████████████████████████████▊ | 2396/3121 [00:13<00:04, 181.16it/s]
78%|███████████████████████████████████████████████████████████████████████████████████████▌ | 2419/3121 [00:13<00:03, 194.62it/s]
78%|████████████████████████████████████████████████████████████████████████████████████████▎ | 2439/3121 [00:14<00:03, 179.90it/s]
79%|████████████████████████████████████████████████████████████████████████████████████████▉ | 2458/3121 [00:14<00:03, 177.38it/s]
79%|█████████████████████████████████████████████████████████████████████████████████████████▋ | 2476/3121 [00:14<00:03, 172.83it/s]
80%|██████████████████████████████████████████████████████████████████████████████████████████▎ | 2494/3121 [00:14<00:03, 161.72it/s]
80%|██████████████████████████████████████████████████████████████████████████████████████████▉ | 2512/3121 [00:14<00:03, 165.32it/s]
81%|███████████████████████████████████████████████████████████████████████████████████████████▌ | 2529/3121 [00:14<00:04, 147.41it/s]
82%|████████████████████████████████████████████████████████████████████████████████████████████▏ | 2545/3121 [00:14<00:04, 138.19it/s]
82%|████████████████████████████████████████████████████████████████████████████████████████████▋ | 2561/3121 [00:14<00:03, 143.48it/s]
83%|█████████████████████████████████████████████████████████████████████████████████████████████▍ | 2580/3121 [00:15<00:03, 155.47it/s]
83%|██████████████████████████████████████████████████████████████████████████████████████████████▏ | 2601/3121 [00:15<00:03, 170.03it/s]
84%|██████████████████████████████████████████████████████████████████████████████████████████████▉ | 2622/3121 [00:15<00:02, 180.76it/s]
85%|███████████████████████████████████████████████████████████████████████████████████████████████▌ | 2641/3121 [00:15<00:02, 173.02it/s]
85%|████████████████████████████████████████████████████████████████████████████████████████████████▎ | 2659/3121 [00:15<00:02, 170.69it/s]
86%|████████████████████████████████████████████████████████████████████████████████████████████████▉ | 2677/3121 [00:15<00:02, 167.23it/s]
86%|█████████████████████████████████████████████████████████████████████████████████████████████████▌ | 2695/3121 [00:15<00:02, 170.31it/s]
87%|██████████████████████████████████████████████████████████████████████████████████████████████████▏ | 2713/3121 [00:15<00:02, 168.13it/s]
87%|██████████████████████████████████████████████████████████████████████████████████████████████████▊ | 2730/3121 [00:15<00:02, 159.18it/s]
88%|███████████████████████████████████████████████████████████████████████████████████████████████████▍ | 2747/3121 [00:16<00:02, 161.80it/s]
89%|████████████████████████████████████████████████████████████████████████████████████████████████████ | 2764/3121 [00:16<00:02, 159.15it/s]
89%|████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 2787/3121 [00:16<00:01, 178.68it/s]
90%|█████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 2806/3121 [00:16<00:01, 176.41it/s]
90%|██████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 2824/3121 [00:16<00:01, 177.07it/s]
91%|██████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 2842/3121 [00:16<00:01, 172.47it/s]
92%|███████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 2860/3121 [00:16<00:01, 174.15it/s]
92%|████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 2878/3121 [00:16<00:01, 171.37it/s]
93%|████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 2896/3121 [00:16<00:01, 173.41it/s]
93%|█████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 2916/3121 [00:16<00:01, 179.60it/s]
94%|██████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 2936/3121 [00:17<00:01, 184.98it/s]
95%|██████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 2955/3121 [00:17<00:00, 175.58it/s]
95%|███████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 2973/3121 [00:17<00:00, 171.61it/s]
96%|████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 2991/3121 [00:17<00:00, 173.56it/s]
96%|████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 3009/3121 [00:17<00:00, 170.06it/s]
97%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 3027/3121 [00:17<00:00, 167.64it/s]
98%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 3044/3121 [00:17<00:00, 159.66it/s]
98%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 3061/3121 [00:17<00:00, 157.78it/s]
99%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 3080/3121 [00:17<00:00, 165.43it/s]
99%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏| 3097/3121 [00:18<00:00, 157.44it/s]
100%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋| 3113/3121 [00:18<00:00, 154.44it/s]
100%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 3121/3121 [00:18<00:00, 170.95it/s]
We can now compare the kurtosis measures obtained with the constrained fit to the measures obtained before, where we see that many of the artefactual voxels have now been corrected. In particular outliers caused by pure noise – instead of for example acquisition artefacts – can be corrected with this method.
compare_maps([dkifit_plus], ['mk', 'ak', 'rk'], fit_labels=['DKI+'],
filename='Kurtosis_tensor_standard_measures_plus.png')
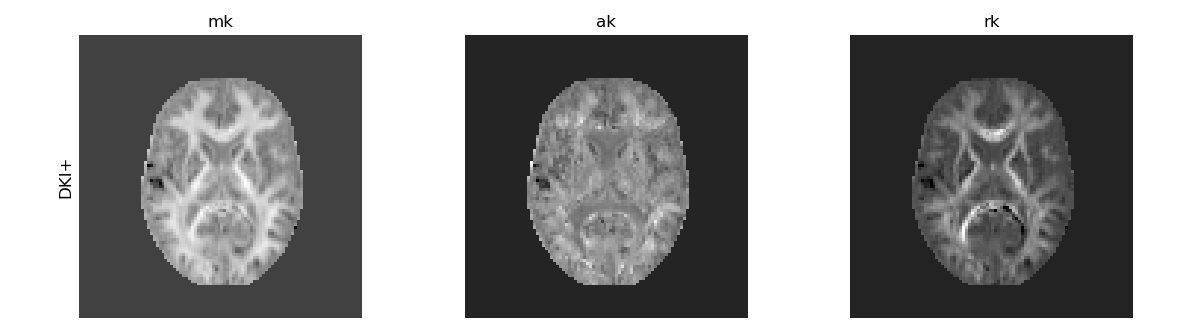
DKI standard kurtosis measures obtained with constrained optimization.
When using constrained optimization, the expected range of the kurtosis measures is also naturally constrained, and so does not typically require additional clipping.
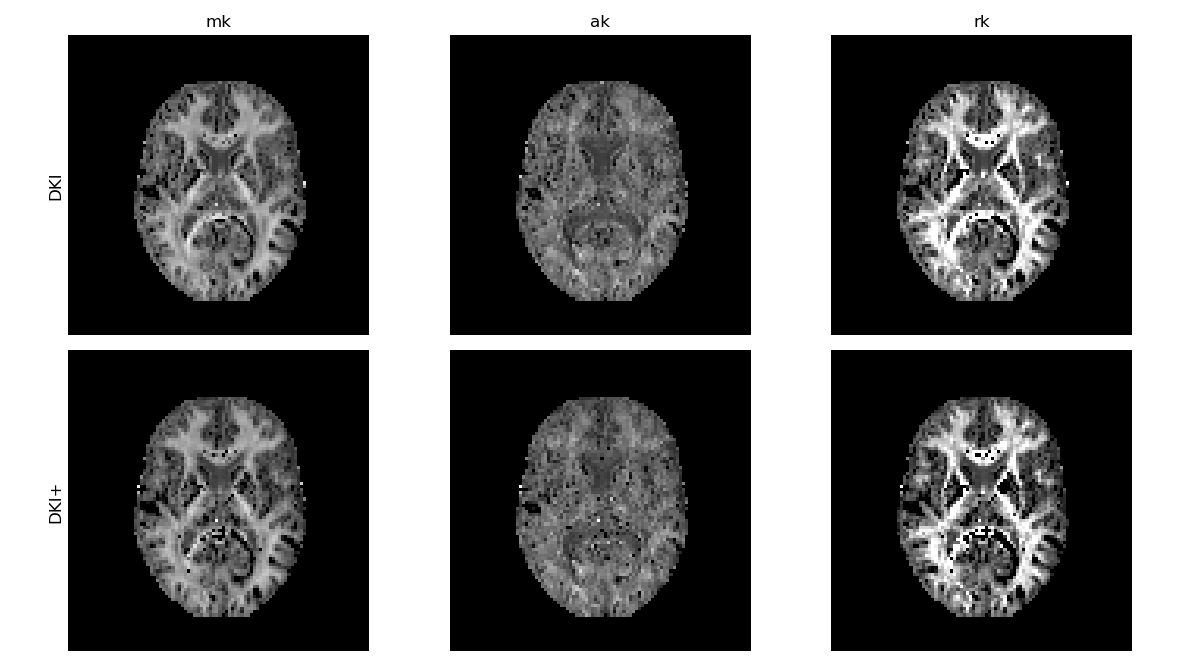
Finally, constrained optimization obviates the need for smoothing in many cases:
dkifit_noisy = dkimodel.fit(data[:, :, 9:10], mask=mask)
dkifit_noisy_plus = dkimodel_plus.fit(data[:, :, 9:10], mask=mask)
compare_maps([dkifit_noisy, dkifit_noisy_plus], ['mk', 'ak', 'rk'],
fit_labels=['DKI', 'DKI+'], map_kwargs={'vmin': 0, 'vmax': 1.5},
filename='Kurtosis_tensor_standard_measures_noisy.png')
0%| | 0/3121 [00:00<?, ?it/s]
3%|███▎ | 89/3121 [00:00<00:03, 878.79it/s]
6%|██████▍ | 177/3121 [00:00<00:04, 717.81it/s]
8%|█████████▏ | 251/3121 [00:00<00:04, 693.96it/s]
11%|████████████ | 329/3121 [00:00<00:03, 723.20it/s]
13%|███████████████ | 414/3121 [00:00<00:03, 762.11it/s]
16%|█████████████████▉ | 491/3121 [00:00<00:03, 761.38it/s]
19%|█████████████████████▌ | 589/3121 [00:00<00:03, 810.15it/s]
22%|████████████████████████▋ | 676/3121 [00:00<00:02, 826.16it/s]
24%|███████████████████████████▊ | 762/3121 [00:00<00:02, 834.26it/s]
27%|██████████████████████████████▉ | 846/3121 [00:01<00:02, 828.25it/s]
30%|██████████████████████████████████▎ | 939/3121 [00:01<00:02, 855.45it/s]
33%|█████████████████████████████████████ | 1025/3121 [00:01<00:02, 853.73it/s]
36%|████████████████████████████████████████▎ | 1115/3121 [00:01<00:02, 864.52it/s]
39%|███████████████████████████████████████████▌ | 1204/3121 [00:01<00:02, 869.37it/s]
41%|██████████████████████████████████████████████▉ | 1295/3121 [00:01<00:02, 879.16it/s]
45%|██████████████████████████████████████████████████▍ | 1393/3121 [00:01<00:01, 906.40it/s]
48%|█████████████████████████████████████████████████████▉ | 1489/3121 [00:01<00:01, 919.84it/s]
51%|█████████████████████████████████████████████████████████▋ | 1595/3121 [00:01<00:01, 958.48it/s]
54%|█████████████████████████████████████████████████████████████▏ | 1691/3121 [00:01<00:01, 928.14it/s]
57%|████████████████████████████████████████████████████████████████▋ | 1785/3121 [00:02<00:01, 902.43it/s]
60%|███████████████████████████████████████████████████████████████████▉ | 1876/3121 [00:02<00:01, 876.41it/s]
63%|███████████████████████████████████████████████████████████████████████▌ | 1978/3121 [00:02<00:01, 914.66it/s]
66%|██████████████████████████████████████████████████████████████████████████▉ | 2070/3121 [00:02<00:01, 914.51it/s]
69%|██████████████████████████████████████████████████████████████████████████████▎ | 2162/3121 [00:02<00:01, 913.65it/s]
72%|█████████████████████████████████████████████████████████████████████████████████▌ | 2254/3121 [00:02<00:00, 886.62it/s]
75%|████████████████████████████████████████████████████████████████████████████████████▊ | 2343/3121 [00:02<00:00, 885.07it/s]
78%|████████████████████████████████████████████████████████████████████████████████████████ | 2432/3121 [00:02<00:00, 884.75it/s]
81%|███████████████████████████████████████████████████████████████████████████████████████████▎ | 2521/3121 [00:02<00:00, 884.40it/s]
84%|██████████████████████████████████████████████████████████████████████████████████████████████▍ | 2610/3121 [00:03<00:00, 883.65it/s]
87%|█████████████████████████████████████████████████████████████████████████████████████████████████▊ | 2702/3121 [00:03<00:00, 892.12it/s]
89%|█████████████████████████████████████████████████████████████████████████████████████████████████████ | 2792/3121 [00:03<00:00, 891.01it/s]
93%|████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 2888/3121 [00:03<00:00, 907.68it/s]
96%|████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 2995/3121 [00:03<00:00, 953.52it/s]
99%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏| 3097/3121 [00:03<00:00, 970.92it/s]
100%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 3121/3121 [00:03<00:00, 878.66it/s]
0%| | 0/3121 [00:00<?, ?it/s]C:\Users\skoudoro\AppData\Local\Continuum\Anaconda3\envs\py310\lib\site-packages\cvxpy\problems\problem.py:1387: UserWarning: Solution may be inaccurate. Try another solver, adjusting the solver settings, or solve with verbose=True for more information.
warnings.warn(
C:\Users\skoudoro\Devel\dipy\dipy\core\optimize.py:527: UserWarning: Solver failed to produce an optimum: optimal_inaccurate.
warnings.warn(msg)
0%|▎ | 10/3121 [00:01<10:18, 5.03it/s]
0%|▍ | 11/3121 [00:03<19:13, 2.70it/s]
1%|▊ | 23/3121 [00:03<06:23, 8.07it/s]
1%|█ | 30/3121 [00:05<08:56, 5.76it/s]
1%|█▎ | 34/3121 [00:07<11:56, 4.31it/s]
2%|█▊ | 48/3121 [00:08<08:43, 5.87it/s]
2%|█▉ | 53/3121 [00:10<10:19, 4.96it/s]
2%|██▏ | 58/3121 [00:12<12:16, 4.16it/s]
2%|██▊ | 74/3121 [00:12<06:04, 8.37it/s]
3%|███▎ | 89/3121 [00:14<05:51, 8.62it/s]
3%|███▍ | 94/3121 [00:17<10:23, 4.86it/s]
4%|████ | 111/3121 [00:17<05:53, 8.51it/s]
4%|████▋ | 126/3121 [00:17<03:53, 12.84it/s]
5%|█████▎ | 145/3121 [00:17<02:26, 20.26it/s]
5%|█████▊ | 159/3121 [00:17<01:49, 27.00it/s]
6%|██████▌ | 177/3121 [00:17<01:16, 38.40it/s]
6%|███████▎ | 197/3121 [00:17<00:54, 53.50it/s]
7%|███████▊ | 213/3121 [00:18<00:43, 66.21it/s]
7%|████████▌ | 231/3121 [00:18<00:34, 82.75it/s]
8%|█████████▏ | 248/3121 [00:18<00:30, 95.65it/s]
9%|█████████▋ | 266/3121 [00:18<00:25, 111.86it/s]
9%|██████████▎ | 283/3121 [00:18<00:23, 119.60it/s]
10%|███████████ | 304/3121 [00:18<00:20, 139.40it/s]
10%|███████████▊ | 322/3121 [00:18<00:18, 148.96it/s]
11%|████████████▍ | 340/3121 [00:18<00:17, 156.66it/s]
11%|█████████████ | 358/3121 [00:18<00:16, 162.56it/s]
12%|█████████████▋ | 376/3121 [00:19<00:17, 158.98it/s]
13%|██████████████▎ | 393/3121 [00:19<00:16, 160.66it/s]
13%|██████████████▉ | 410/3121 [00:19<00:17, 154.11it/s]
14%|███████████████▌ | 426/3121 [00:19<00:17, 153.87it/s]
14%|████████████████▎ | 445/3121 [00:19<00:16, 161.17it/s]
15%|████████████████▉ | 462/3121 [00:19<00:16, 157.87it/s]
15%|█████████████████▍ | 478/3121 [00:19<00:16, 158.18it/s]
16%|██████████████████ | 494/3121 [00:19<00:17, 153.82it/s]
16%|██████████████████▋ | 513/3121 [00:19<00:15, 163.74it/s]
17%|███████████████████▎ | 530/3121 [00:20<00:15, 165.17it/s]
18%|████████████████████▏ | 553/3121 [00:20<00:13, 183.50it/s]
18%|████████████████████▉ | 572/3121 [00:20<00:13, 184.93it/s]
19%|█████████████████████▌ | 591/3121 [00:20<00:14, 180.56it/s]
20%|██████████████████████▎ | 610/3121 [00:20<00:14, 177.73it/s]
20%|██████████████████████▉ | 628/3121 [00:20<00:14, 177.93it/s]
21%|███████████████████████▌ | 646/3121 [00:20<00:14, 173.06it/s]
21%|████████████████████████▎ | 664/3121 [00:20<00:14, 165.05it/s]
22%|████████████████████████▊ | 681/3121 [00:20<00:15, 160.56it/s]
22%|█████████████████████████▍ | 698/3121 [00:20<00:15, 155.34it/s]
23%|██████████████████████████ | 714/3121 [00:21<00:15, 156.31it/s]
24%|██████████████████████████▊ | 734/3121 [00:21<00:14, 168.17it/s]
24%|███████████████████████████▍ | 751/3121 [00:21<00:14, 163.53it/s]
25%|████████████████████████████ | 768/3121 [00:21<00:14, 163.02it/s]
25%|████████████████████████████▋ | 786/3121 [00:21<00:14, 165.66it/s]
26%|█████████████████████████████▍ | 805/3121 [00:21<00:13, 171.27it/s]
27%|██████████████████████████████▎ | 831/3121 [00:21<00:11, 194.76it/s]
27%|███████████████████████████████▏ | 855/3121 [00:21<00:11, 203.12it/s]
28%|███████████████████████████████▉ | 876/3121 [00:21<00:11, 189.22it/s]
29%|████████████████████████████████▊ | 898/3121 [00:22<00:11, 196.09it/s]
29%|█████████████████████████████████▌ | 918/3121 [00:22<00:12, 181.35it/s]
30%|██████████████████████████████████▏ | 937/3121 [00:22<00:12, 173.80it/s]
31%|██████████████████████████████████▉ | 955/3121 [00:22<00:12, 175.07it/s]
31%|███████████████████████████████████▌ | 973/3121 [00:22<00:12, 175.97it/s]
32%|████████████████████████████████████▏ | 991/3121 [00:22<00:12, 171.72it/s]
32%|████████████████████████████████████▌ | 1009/3121 [00:22<00:12, 173.56it/s]
33%|█████████████████████████████████████▏ | 1027/3121 [00:22<00:12, 166.30it/s]
34%|█████████████████████████████████████▊ | 1046/3121 [00:22<00:12, 171.51it/s]
34%|██████████████████████████████████████▌ | 1064/3121 [00:23<00:11, 173.57it/s]
35%|███████████████████████████████████████▎ | 1087/3121 [00:23<00:10, 189.28it/s]
35%|████████████████████████████████████████ | 1107/3121 [00:23<00:10, 186.44it/s]
36%|████████████████████████████████████████▊ | 1126/3121 [00:23<00:11, 178.06it/s]
37%|█████████████████████████████████████████▍ | 1144/3121 [00:23<00:11, 168.32it/s]
37%|██████████████████████████████████████████ | 1161/3121 [00:23<00:12, 154.70it/s]
38%|██████████████████████████████████████████▌ | 1177/3121 [00:23<00:12, 155.77it/s]
38%|███████████████████████████████████████████▏ | 1194/3121 [00:23<00:12, 159.22it/s]
39%|███████████████████████████████████████████▉ | 1212/3121 [00:23<00:11, 164.65it/s]
39%|████████████████████████████████████████████▍ | 1229/3121 [00:24<00:12, 157.64it/s]
40%|█████████████████████████████████████████████ | 1245/3121 [00:24<00:12, 152.70it/s]
40%|█████████████████████████████████████████████▋ | 1261/3121 [00:24<00:12, 154.39it/s]
41%|██████████████████████████████████████████████▏ | 1277/3121 [00:24<00:11, 155.73it/s]
41%|██████████████████████████████████████████████▊ | 1293/3121 [00:24<00:12, 152.25it/s]
42%|███████████████████████████████████████████████▌ | 1313/3121 [00:24<00:10, 165.44it/s]
43%|████████████████████████████████████████████████▎ | 1334/3121 [00:24<00:10, 177.88it/s]
44%|█████████████████████████████████████████████████▏ | 1358/3121 [00:24<00:09, 195.61it/s]
44%|██████████████████████████████████████████████████ | 1384/3121 [00:24<00:08, 212.82it/s]
45%|███████████████████████████████████████████████████▎ | 1406/3121 [00:26<00:49, 34.70it/s]
46%|███████████████████████████████████████████████████▉ | 1422/3121 [00:26<00:39, 42.63it/s]
46%|████████████████████████████████████████████████████▌ | 1439/3121 [00:26<00:31, 53.17it/s]
47%|█████████████████████████████████████████████████████▏ | 1455/3121 [00:27<00:26, 63.24it/s]
47%|█████████████████████████████████████████████████████▊ | 1472/3121 [00:27<00:21, 76.74it/s]
48%|██████████████████████████████████████████████████████▍ | 1491/3121 [00:27<00:17, 94.26it/s]
48%|██████████████████████████████████████████████████████▋ | 1511/3121 [00:27<00:14, 113.34it/s]
49%|███████████████████████████████████████████████████████▎ | 1529/3121 [00:27<00:12, 124.32it/s]
50%|████████████████████████████████████████████████████████▌ | 1547/3121 [00:29<00:57, 27.42it/s]
50%|█████████████████████████████████████████████████████████ | 1563/3121 [00:29<00:44, 35.33it/s]
51%|█████████████████████████████████████████████████████████▋ | 1581/3121 [00:29<00:32, 46.72it/s]
51%|██████████████████████████████████████████████████████████▎ | 1596/3121 [00:31<01:11, 21.25it/s]
52%|██████████████████████████████████████████████████████████▊ | 1609/3121 [00:32<01:38, 15.28it/s]
52%|███████████████████████████████████████████████████████████ | 1617/3121 [00:34<02:14, 11.20it/s]
52%|███████████████████████████████████████████████████████████▊ | 1636/3121 [00:34<01:25, 17.36it/s]
53%|████████████████████████████████████████████████████████████▎ | 1651/3121 [00:34<01:02, 23.58it/s]
53%|████████████████████████████████████████████████████████████▊ | 1666/3121 [00:34<00:46, 31.51it/s]
54%|█████████████████████████████████████████████████████████████▌ | 1684/3121 [00:34<00:32, 43.71it/s]
54%|██████████████████████████████████████████████████████████████ | 1700/3121 [00:35<00:25, 55.90it/s]
55%|██████████████████████████████████████████████████████████████▋ | 1717/3121 [00:35<00:19, 70.72it/s]
56%|███████████████████████████████████████████████████████████████▍ | 1736/3121 [00:35<00:15, 89.34it/s]
56%|███████████████████████████████████████████████████████████████▋ | 1758/3121 [00:35<00:12, 113.05it/s]
57%|████████████████████████████████████████████████████████████████▎ | 1776/3121 [00:35<00:10, 123.81it/s]
57%|████████████████████████████████████████████████████████████████▉ | 1794/3121 [00:35<00:10, 124.78it/s]
58%|█████████████████████████████████████████████████████████████████▌ | 1810/3121 [00:35<00:09, 132.27it/s]
59%|██████████████████████████████████████████████████████████████████▍ | 1836/3121 [00:35<00:07, 162.95it/s]
59%|███████████████████████████████████████████████████████████████████▏ | 1855/3121 [00:35<00:07, 161.25it/s]
60%|███████████████████████████████████████████████████████████████████▉ | 1875/3121 [00:35<00:07, 170.80it/s]
61%|████████████████████████████████████████████████████████████████████▌ | 1895/3121 [00:36<00:06, 178.15it/s]
61%|█████████████████████████████████████████████████████████████████████▍ | 1917/3121 [00:36<00:06, 189.35it/s]
62%|██████████████████████████████████████████████████████████████████████▏ | 1939/3121 [00:36<00:05, 197.56it/s]
63%|██████████████████████████████████████████████████████████████████████▉ | 1960/3121 [00:36<00:05, 194.99it/s]
63%|███████████████████████████████████████████████████████████████████████▋ | 1980/3121 [00:36<00:05, 190.44it/s]
64%|████████████████████████████████████████████████████████████████████████▍ | 2000/3121 [00:36<00:06, 177.47it/s]
65%|█████████████████████████████████████████████████████████████████████████ | 2019/3121 [00:36<00:06, 171.09it/s]
65%|█████████████████████████████████████████████████████████████████████████▊ | 2037/3121 [00:36<00:06, 164.24it/s]
66%|██████████████████████████████████████████████████████████████████████████▎ | 2054/3121 [00:37<00:07, 136.54it/s]
66%|██████████████████████████████████████████████████████████████████████████▉ | 2071/3121 [00:37<00:07, 144.27it/s]
67%|███████████████████████████████████████████████████████████████████████████▋ | 2091/3121 [00:37<00:06, 158.17it/s]
68%|████████████████████████████████████████████████████████████████████████████▎ | 2108/3121 [00:37<00:06, 159.60it/s]
68%|█████████████████████████████████████████████████████████████████████████████ | 2130/3121 [00:37<00:05, 172.38it/s]
69%|█████████████████████████████████████████████████████████████████████████████▊ | 2148/3121 [00:37<00:05, 164.92it/s]
69%|██████████████████████████████████████████████████████████████████████████████▍ | 2166/3121 [00:37<00:05, 168.11it/s]
70%|███████████████████████████████████████████████████████████████████████████████▎ | 2189/3121 [00:37<00:05, 185.32it/s]
71%|███████████████████████████████████████████████████████████████████████████████▉ | 2208/3121 [00:37<00:05, 167.11it/s]
71%|████████████████████████████████████████████████████████████████████████████████▌ | 2226/3121 [00:38<00:05, 170.17it/s]
72%|█████████████████████████████████████████████████████████████████████████████████▍ | 2248/3121 [00:38<00:04, 183.47it/s]
73%|██████████████████████████████████████████████████████████████████████████████████ | 2267/3121 [00:38<00:04, 184.86it/s]
73%|██████████████████████████████████████████████████████████████████████████████████▊ | 2286/3121 [00:38<00:04, 181.74it/s]
74%|███████████████████████████████████████████████████████████████████████████████████▍ | 2305/3121 [00:38<00:04, 182.61it/s]
74%|████████████████████████████████████████████████████████████████████████████████████▏ | 2325/3121 [00:38<00:04, 187.18it/s]
75%|█████████████████████████████████████████████████████████████████████████████████████ | 2348/3121 [00:38<00:03, 199.22it/s]
76%|█████████████████████████████████████████████████████████████████████████████████████▊ | 2369/3121 [00:38<00:04, 185.47it/s]
77%|██████████████████████████████████████████████████████████████████████████████████████▍ | 2388/3121 [00:38<00:04, 171.82it/s]
77%|███████████████████████████████████████████████████████████████████████████████████████ | 2406/3121 [00:39<00:04, 173.59it/s]
78%|███████████████████████████████████████████████████████████████████████████████████████▊ | 2426/3121 [00:39<00:03, 180.38it/s]
78%|████████████████████████████████████████████████████████████████████████████████████████▌ | 2445/3121 [00:39<00:03, 172.82it/s]
79%|█████████████████████████████████████████████████████████████████████████████████████████▏ | 2463/3121 [00:39<00:03, 174.38it/s]
79%|█████████████████████████████████████████████████████████████████████████████████████████▊ | 2481/3121 [00:39<00:03, 166.10it/s]
80%|██████████████████████████████████████████████████████████████████████████████████████████▍ | 2498/3121 [00:39<00:03, 163.17it/s]
81%|███████████████████████████████████████████████████████████████████████████████████████████ | 2515/3121 [00:39<00:03, 163.69it/s]
81%|███████████████████████████████████████████████████████████████████████████████████████████▋ | 2533/3121 [00:39<00:03, 164.08it/s]
82%|████████████████████████████████████████████████████████████████████████████████████████████▎ | 2551/3121 [00:39<00:03, 168.10it/s]
83%|█████████████████████████████████████████████████████████████████████████████████████████████▎ | 2577/3121 [00:40<00:02, 194.01it/s]
83%|██████████████████████████████████████████████████████████████████████████████████████████████ | 2597/3121 [00:40<00:02, 188.52it/s]
84%|██████████████████████████████████████████████████████████████████████████████████████████████▋ | 2616/3121 [00:40<00:02, 178.20it/s]
84%|███████████████████████████████████████████████████████████████████████████████████████████████▎ | 2634/3121 [00:40<00:02, 178.34it/s]
85%|████████████████████████████████████████████████████████████████████████████████████████████████ | 2652/3121 [00:40<00:02, 168.72it/s]
86%|████████████████████████████████████████████████████████████████████████████████████████████████▋ | 2670/3121 [00:40<00:02, 162.42it/s]
86%|█████████████████████████████████████████████████████████████████████████████████████████████████▎ | 2688/3121 [00:40<00:02, 166.82it/s]
87%|█████████████████████████████████████████████████████████████████████████████████████████████████▉ | 2706/3121 [00:40<00:02, 170.17it/s]
87%|██████████████████████████████████████████████████████████████████████████████████████████████████▋ | 2724/3121 [00:40<00:02, 163.22it/s]
88%|███████████████████████████████████████████████████████████████████████████████████████████████████▏ | 2741/3121 [00:41<00:02, 163.01it/s]
88%|████████████████████████████████████████████████████████████████████████████████████████████████████ | 2762/3121 [00:41<00:02, 173.13it/s]
89%|████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 2780/3121 [00:41<00:01, 174.72it/s]
90%|█████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 2798/3121 [00:41<00:01, 170.88it/s]
90%|██████████████████████████████████████████████████████████████████████████████████████████████████████ | 2818/3121 [00:41<00:01, 178.81it/s]
91%|██████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 2837/3121 [00:41<00:01, 181.62it/s]
92%|███████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 2856/3121 [00:41<00:01, 179.47it/s]
92%|████████████████████████████████████████████████████████████████████████████████████████████████████████ | 2874/3121 [00:41<00:01, 163.76it/s]
93%|████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 2894/3121 [00:41<00:01, 173.26it/s]
93%|█████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 2912/3121 [00:41<00:01, 165.41it/s]
94%|██████████████████████████████████████████████████████████████████████████████████████████████████████████ | 2930/3121 [00:42<00:01, 169.10it/s]
94%|██████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 2948/3121 [00:42<00:01, 167.10it/s]
95%|███████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 2965/3121 [00:42<00:00, 162.91it/s]
96%|███████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 2982/3121 [00:42<00:00, 164.52it/s]
96%|████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 2999/3121 [00:42<00:00, 161.08it/s]
97%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 3016/3121 [00:42<00:00, 158.65it/s]
97%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 3032/3121 [00:42<00:00, 158.56it/s]
98%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 3048/3121 [00:42<00:00, 149.89it/s]
98%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 3064/3121 [00:44<00:02, 27.06it/s]
99%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 3081/3121 [00:44<00:01, 36.40it/s]
99%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 3094/3121 [00:46<00:01, 18.28it/s]
100%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍| 3106/3121 [00:48<00:01, 12.43it/s]
100%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋| 3113/3121 [00:50<00:00, 8.94it/s]
100%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉| 3118/3121 [00:55<00:00, 3.97it/s]
100%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 3121/3121 [00:57<00:00, 54.69it/s]
DKI standard kurtosis measures obtained on unsmoothed data with constrained optimization.
Mean kurtosis tensor and kurtosis fractional anisotropy#
As pointed by previous studies [Hansen2013], axial, radial and mean kurtosis depends on the information of both diffusion and kurtosis tensor. DKI measures that only depend on the kurtosis tensor include the mean of the kurtosis tensor [Hansen2013], and the kurtosis fractional anisotropy [GlennR2015]. These measures are computed and illustrated below:
compare_maps([dkifit_plus], ['mkt', 'kfa'], fit_labels=['DKI+'],
map_kwargs=[{'vmin': 0, 'vmax': 1.5}, {'vmin': 0, 'vmax': 1}],
filename='Measures_from_kurtosis_tensor_only.png')
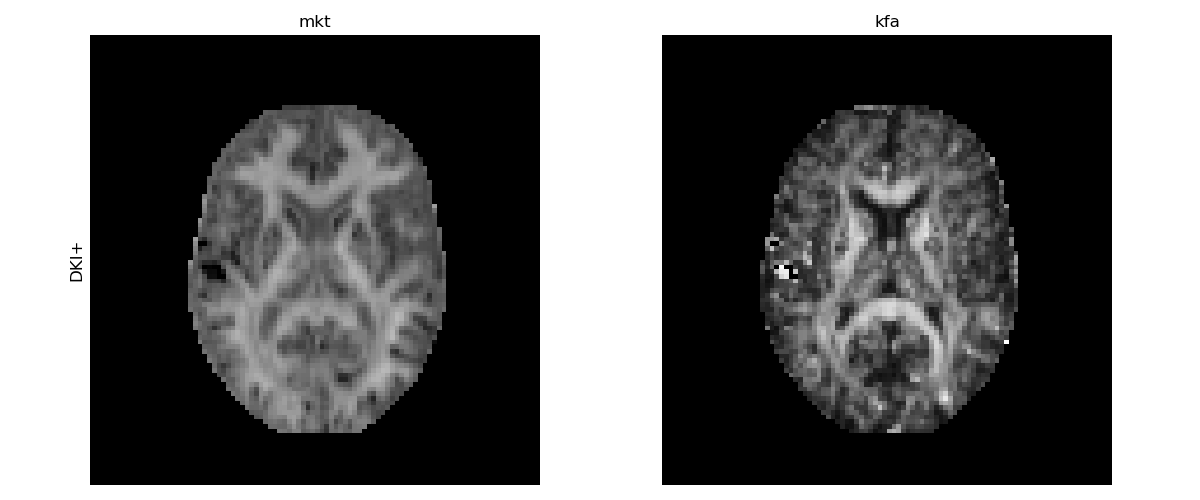
DKI measures obtained from the kurtosis tensor only.
As reported by [Hansen2013], the mean of the kurtosis tensor (MKT) produces similar maps than the standard mean kurtosis (MK). On the other hand, the kurtosis fractional anisotropy (KFA) maps shows that the kurtosis tensor have different degrees of anisotropy than the FA measures from the diffusion tensor.
References#
Jensen JH, Helpern JA, Ramani A, Lu H, Kaczynski K (2005). Diffusional Kurtosis Imaging: The Quantification of Non_Gaussian Water Diffusion by Means of Magnetic Resonance Imaging. Magnetic Resonance in Medicine 53: 1432-1440
Jensen JH, Helpern JA (2010). MRI quantification of non-Gaussian water diffusion by kurtosis analysis. NMR in Biomedicine 23(7): 698-710
Fieremans E, Jensen JH, Helpern JA (2011). White matter characterization with diffusion kurtosis imaging. NeuroImage 58: 177-188
Veraart J, Poot DH, Van Hecke W, Blockx I, Van der Linden A, Verhoye M, Sijbers J (2011). More Accurate Estimation of Diffusion Tensor Parameters Using Diffusion Kurtosis Imaging. Magnetic Resonance in Medicine 65(1): 138-145
Neto Henriques R, Ferreira H, Correia M, (2012). Diffusion kurtosis imaging of the healthy human brain. Master Dissertation Bachelor and Master Programin Biomedical Engineering and Biophysics, Faculty of Sciences. https://repositorio.ul.pt/bitstream/10451/8511/1/ulfc104137_tm_Rafael_Henriques.pdf
Hansen B, Lund TE, Sangill R, and Jespersen SN (2013). Experimentally and computationally393fast method for estimation of a mean kurtosis. Magnetic Resonance in Medicine 69, 1754–1760.394doi:10.1002/mrm.24743
Glenn GR, Helpern JA, Tabesh A, Jensen JH (2015). Quantitative assessment of diffusional387kurtosis anisotropy. NMR in Biomedicine28, 448–459. doi:10.1002/nbm.3271
Neto Henriques R, Correia MM, Nunes RG, Ferreira HA (2015). Exploring the 3D geometry of the diffusion kurtosis tensor - Impact on the development of robust tractography procedures and novel biomarkers, NeuroImage 111: 85-99
Perrone D, Aelterman J, Pižurica A, Jeurissen B, Philips W, Leemans A, (2015). The effect of Gibbs ringing artifacts on measures derived from diffusion MRI. Neuroimage 120, 441-455. https://doi.org/10.1016/j.neuroimage.2015.06.068.
Tax CMW, Otte WM, Viergever MA, Dijkhuizen RM, Leemans A (2014). REKINDLE: Robust extraction of kurtosis INDices with linear estimation. Magnetic Resonance in Medicine 73(2): 794-808.
Hansen, B, Jespersen, SN (2016). Data for evaluation of fast kurtosis strategies, b-value optimization and exploration of diffusion MRI contrast. Scientific Data 3: 160072 doi:10.1038/sdata.2016.72
Neto Henriques R (2018). Advanced Methods for Diffusion MRI Data Analysis and their Application to the Healthy Ageing Brain (Doctoral thesis). https://doi.org/10.17863/CAM.29356
Total running time of the script: (2 minutes 22.283 seconds)