Note
Go to the end to download the full example code
Denoise images using Adaptive Soft Coefficient Matching (ASCM)#
The adaptive soft coefficient matching (ASCM) as described in [1] is an improved extension of non-local means (NLMEANS) denoising. ASCM gives a better denoised images from two standard non-local means denoised versions of the original data with different degrees sharpness. Here, one denoised input is more “smooth” than the other (the easiest way to achieve this denoising is use non_local_means with two different patch radii).
ASCM involves these basic steps
Computes wavelet decomposition of the noisy as well as denoised inputs
Combines the wavelets for the output image in a way that it takes it’s smoothness (low frequency components) from the input with larger smoothing, and the sharp features (high frequency components) from the input with less smoothing.
This way ASCM gives us a well denoised output while preserving the sharpness of the image features.
Let us load the necessary modules
from time import time
import matplotlib.pyplot as plt
import numpy as np
from dipy.core.gradients import gradient_table
from dipy.data import get_fnames
from dipy.denoise.adaptive_soft_matching import adaptive_soft_matching
from dipy.denoise.noise_estimate import estimate_sigma
from dipy.denoise.non_local_means import non_local_means
from dipy.io.gradients import read_bvals_bvecs
from dipy.io.image import load_nifti, save_nifti
Choose one of the data from the datasets in dipy
dwi_fname, dwi_bval_fname, dwi_bvec_fname = get_fnames(name="sherbrooke_3shell")
data, affine = load_nifti(dwi_fname)
bvals, bvecs = read_bvals_bvecs(dwi_bval_fname, dwi_bvec_fname)
gtab = gradient_table(bvals, bvecs=bvecs)
mask = data[..., 0] > 80
data = data[..., 1]
print("vol size", data.shape)
t = time()
vol size (128, 128, 60)
In order to generate the two pre-denoised versions of the data we will use
the non_local_means denoining # noqa: E501
For non_local_means first we need to estimate the standard deviation of
the noise. We use N=4 since the Sherbrooke dataset was acquired on a
1.5T Siemens scanner with a 4 array head coil.
sigma = estimate_sigma(data, N=4)
For the denoised version of the original data which preserves sharper features, we perform non-local means with smaller patch size.
den_small = non_local_means(
data, sigma=sigma, mask=mask, patch_radius=1, block_radius=1, rician=True
)
For the denoised version of the original data that implies more smoothing, we perform non-local means with larger patch size.
den_large = non_local_means(
data, sigma=sigma, mask=mask, patch_radius=2, block_radius=1, rician=True
)
Now we perform the adaptive soft coefficient matching. Empirically we set the adaptive parameter in ascm to be the average of the local noise variance, in this case the sigma itself.
den_final = adaptive_soft_matching(data, den_small, den_large, sigma[0])
print("total time", time() - t)
total time 9.443907260894775
To access the quality of this denoising procedure, we plot an axial slice of the original data, it’s denoised output and residuals.
axial_middle = data.shape[2] // 2
original = data[:, :, axial_middle].T
final_output = den_final[:, :, axial_middle].T
difference = np.abs(final_output.astype(np.float64) - original.astype(np.float64))
difference[~mask[:, :, axial_middle].T] = 0
fig, ax = plt.subplots(1, 3)
ax[0].imshow(original, cmap="gray", origin="lower")
ax[0].set_title("Original")
ax[1].imshow(final_output, cmap="gray", origin="lower")
ax[1].set_title("ASCM output")
ax[2].imshow(difference, cmap="gray", origin="lower")
ax[2].set_title("Residual")
for i in range(3):
ax[i].set_axis_off()
plt.savefig("denoised_ascm.png", bbox_inches="tight")
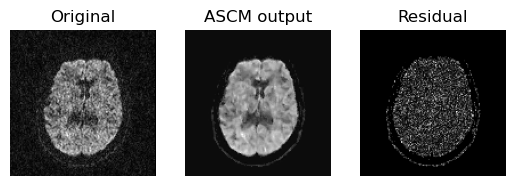
Showing the axial slice without (left) and with (middle) ASCM denoising.
From the above figure we can see that the residual is really uniform in
nature which dictates that ASCM denoises the data while preserving the
sharpness of the features. Now, we are Saving the entire denoised output in
denoised_ascm.nii.gz file.
save_nifti("denoised_ascm.nii.gz", den_final, affine)
For comparison propose we also plot the outputs of the non_local_means
(both with the larger as well as with the smaller patch radius) with the ASCM
output.
fig, ax = plt.subplots(1, 4)
ax[0].imshow(original, cmap="gray", origin="lower")
ax[0].set_title("Original")
ax[1].imshow(
den_small[..., axial_middle].T, cmap="gray", origin="lower", interpolation="none"
)
ax[1].set_title("NLMEANS small")
ax[2].imshow(
den_large[..., axial_middle].T, cmap="gray", origin="lower", interpolation="none"
)
ax[2].set_title("NLMEANS large")
ax[3].imshow(final_output, cmap="gray", origin="lower", interpolation="none")
ax[3].set_title("ASCM ")
for i in range(4):
ax[i].set_axis_off()
plt.savefig("ascm_comparison.png", bbox_inches="tight")
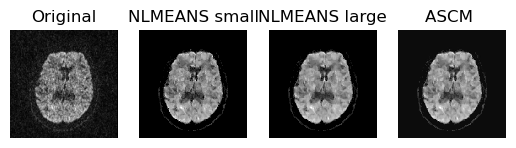
Comparing outputs of the NLMEANS and ASCM.
From the above figure, we can observe that the information of two pre-denoised versions of the raw data, ASCM outperforms standard non-local means in suppressing noise and preserving feature sharpness.
References#
Total running time of the script: (0 minutes 11.980 seconds)