Gradients and Spheres

This example shows how you can create gradient tables and sphere objects using DIPY.

Usually, as we saw in Getting started with DIPY, you load your b-values and b-vectors from disk and then you can create your own gradient table. But this time let’s say that you are an MR physicist and you want to design a new gradient scheme or you are a scientist who wants to simulate many different gradient schemes.

Now let’s assume that you are interested in creating a multi-shell acquisition with 2-shells, one at b=1000 \(s/mm^2\) and one at b=2500 \(s/mm^2\). For both shells let’s say that we want a specific number of gradients (64) and we want to have the points on the sphere evenly distributed.

This is possible using the disperse_charges which is an implementation of electrostatic repulsion Jones et al.[1] .

Let’s start by importing the necessary modules.

import numpy as np

from dipy.core.gradients import gradient_table
from dipy.core.sphere import HemiSphere, Sphere, disperse_charges
from dipy.viz import actor, window

We can first create some random points on a HemiSphere using spherical polar coordinates.

rng = np.random.default_rng()
n_pts = 64
theta = np.pi * rng.random(n_pts)
phi = 2 * np.pi * rng.random(n_pts)
hsph_initial = HemiSphere(theta=theta, phi=phi)

Next, we call disperse_charges which will iteratively move the points so that the electrostatic potential energy is minimized.

hsph_updated, potential = disperse_charges(hsph_initial, 5000)

In hsph_updated we have the updated HemiSphere with the points nicely distributed on the hemisphere. Let’s visualize them.

# Enables/disables interactive visualization
interactive = False

scene = window.Scene()
scene.SetBackground(1, 1, 1)

scene.add(actor.point(hsph_initial.vertices, window.colors.red, point_radius=0.05))
scene.add(actor.point(hsph_updated.vertices, window.colors.green, point_radius=0.05))

window.record(scene=scene, out_path="initial_vs_updated.png", size=(300, 300))
if interactive:
    window.show(scene)

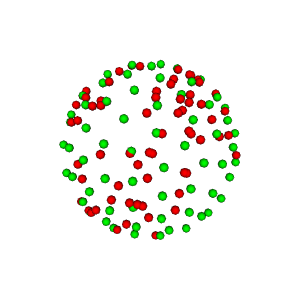
Illustration of electrostatic repulsion of red points which become green points.

We can also create a sphere from the hemisphere and show it in the following way.

sph = Sphere(xyz=np.vstack((hsph_updated.vertices, -hsph_updated.vertices)))

scene.clear()
scene.add(actor.point(sph.vertices, window.colors.green, point_radius=0.05))

window.record(scene=scene, out_path="full_sphere.png", size=(300, 300))
if interactive:
    window.show(scene)

Full sphere.

It is time to create the Gradients. For this purpose we will use the function gradient_table and fill it with the hsph_updated vectors that we created above.

vertices = hsph_updated.vertices
values = np.ones(vertices.shape[0])

We need two stacks of vertices, one for every shell, and we need two sets of b-values, one at 1000 \(s/mm^2\), and one at 2500 \(s/mm^2\), as we discussed previously.

bvecs = np.vstack((vertices, vertices))
bvals = np.hstack((1000 * values, 2500 * values))

We can also add some b0s. Let’s add one at the beginning and one at the end.

bvecs = np.insert(bvecs, (0, bvecs.shape[0]), np.array([0, 0, 0]), axis=0)
bvals = np.insert(bvals, (0, bvals.shape[0]), 0)

print(bvals)
print(bvecs)

[   0. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000.
 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000.
 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000.
 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000.
 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000. 1000.
 1000. 1000. 1000. 1000. 1000. 2500. 2500. 2500. 2500. 2500. 2500. 2500.
 2500. 2500. 2500. 2500. 2500. 2500. 2500. 2500. 2500. 2500. 2500. 2500.
 2500. 2500. 2500. 2500. 2500. 2500. 2500. 2500. 2500. 2500. 2500. 2500.
 2500. 2500. 2500. 2500. 2500. 2500. 2500. 2500. 2500. 2500. 2500. 2500.
 2500. 2500. 2500. 2500. 2500. 2500. 2500. 2500. 2500. 2500. 2500. 2500.
 2500. 2500. 2500. 2500. 2500. 2500. 2500. 2500. 2500.    0.]
[[ 0.          0.          0.        ]
 [ 0.62840912 -0.77023529  0.1088098 ]
 [-0.45508617  0.8611993   0.22634564]
 [-0.32473383  0.11911651  0.93827459]
 [ 0.12027212  0.02644471  0.99238868]
 [ 0.74898275  0.57572682  0.3279687 ]
 [ 0.45859234  0.84960412  0.26051086]
 [ 0.04051051  0.68126793  0.73091238]
 [-0.0735906   0.91534536  0.39588797]
 [ 0.99890043 -0.025384    0.03941549]
 [-0.1019989   0.29394083  0.95036573]
 [ 0.21406095 -0.42504593  0.87949637]
 [-0.90337243 -0.23238568  0.36043743]
 [-0.68031972  0.26206651  0.68446053]
 [-0.31937068 -0.2676325   0.90905182]
 [-0.34248427  0.32023336  0.8832639 ]
 [-0.7999869   0.3489196   0.48813531]
 [ 0.57951898  0.22899749  0.78212397]
 [-0.63088504 -0.7758749   0.00148495]
 [-0.41767139 -0.57622315  0.702508  ]
 [ 0.10130929  0.99375547  0.04675989]
 [-0.80237762 -0.41516512  0.42875177]
 [-0.23477878 -0.06221913  0.97005552]
 [ 0.19783062  0.52356388  0.82870013]
 [ 0.47380843 -0.57212817  0.66945868]
 [-0.08704282 -0.21194403  0.9733978 ]
 [ 0.30874652 -0.23012033  0.92288689]
 [-0.53845368 -0.70344577  0.46393069]
 [ 0.29774511  0.05346423  0.95314712]
 [-0.77124701  0.63444946  0.05149692]
 [-0.62559748 -0.48947088  0.60749161]
 [-0.40408541  0.61550491  0.67665995]
 [-0.17520779 -0.51319826  0.84019627]
 [ 0.89088902  0.43819093  0.11960543]
 [-0.768878   -0.11427646  0.62910056]
 [ 0.39575616  0.20260836  0.89572703]
 [ 0.58890776 -0.32655201  0.73929117]
 [ 0.1143085  -0.17441955  0.978014  ]
 [ 0.95974854 -0.27018392  0.07670325]
 [ 0.1154149   0.26996102  0.9559291 ]
 [-0.60984466  0.07009174  0.78941538]
 [-0.98237224  0.09391583  0.16163104]
 [-0.84609345  0.06482304  0.5290783 ]
 [-0.22448816  0.53299048  0.8157979 ]
 [ 0.12146282 -0.99224489  0.02639829]
 [ 0.19591098 -0.86261727  0.46638004]
 [-0.81558403 -0.54079301  0.20582907]
 [-0.25885426 -0.90287368  0.34323984]
 [ 0.53492121 -0.02637249  0.84449026]
 [ 0.53964131  0.43449257  0.72111266]
 [-0.19449693 -0.6806217   0.70634626]
 [-0.98053881 -0.15801018  0.11651794]
 [-0.7317953  -0.30771257  0.60810248]
 [-0.52046223 -0.33241611  0.78652311]
 [ 0.21408979  0.80786826  0.54910331]
 [-0.93116942  0.16113451  0.32704613]
 [ 0.35270264  0.63898144  0.68359606]
 [ 0.69371315  0.46840791  0.54713445]
 [ 0.68109784 -0.53997035  0.4945076 ]
 [ 0.16962453 -0.72131562  0.67151418]
 [-0.00393353 -0.41503663  0.9097962 ]
 [ 0.87506372  0.34938832  0.33494968]
 [ 0.9594481  -0.08153172  0.26983683]
 [-0.06967638  0.06917517  0.99516833]
 [-0.50608658 -0.10979243  0.85546595]
 [ 0.62840912 -0.77023529  0.1088098 ]
 [-0.45508617  0.8611993   0.22634564]
 [-0.32473383  0.11911651  0.93827459]
 [ 0.12027212  0.02644471  0.99238868]
 [ 0.74898275  0.57572682  0.3279687 ]
 [ 0.45859234  0.84960412  0.26051086]
 [ 0.04051051  0.68126793  0.73091238]
 [-0.0735906   0.91534536  0.39588797]
 [ 0.99890043 -0.025384    0.03941549]
 [-0.1019989   0.29394083  0.95036573]
 [ 0.21406095 -0.42504593  0.87949637]
 [-0.90337243 -0.23238568  0.36043743]
 [-0.68031972  0.26206651  0.68446053]
 [-0.31937068 -0.2676325   0.90905182]
 [-0.34248427  0.32023336  0.8832639 ]
 [-0.7999869   0.3489196   0.48813531]
 [ 0.57951898  0.22899749  0.78212397]
 [-0.63088504 -0.7758749   0.00148495]
 [-0.41767139 -0.57622315  0.702508  ]
 [ 0.10130929  0.99375547  0.04675989]
 [-0.80237762 -0.41516512  0.42875177]
 [-0.23477878 -0.06221913  0.97005552]
 [ 0.19783062  0.52356388  0.82870013]
 [ 0.47380843 -0.57212817  0.66945868]
 [-0.08704282 -0.21194403  0.9733978 ]
 [ 0.30874652 -0.23012033  0.92288689]
 [-0.53845368 -0.70344577  0.46393069]
 [ 0.29774511  0.05346423  0.95314712]
 [-0.77124701  0.63444946  0.05149692]
 [-0.62559748 -0.48947088  0.60749161]
 [-0.40408541  0.61550491  0.67665995]
 [-0.17520779 -0.51319826  0.84019627]
 [ 0.89088902  0.43819093  0.11960543]
 [-0.768878   -0.11427646  0.62910056]
 [ 0.39575616  0.20260836  0.89572703]
 [ 0.58890776 -0.32655201  0.73929117]
 [ 0.1143085  -0.17441955  0.978014  ]
 [ 0.95974854 -0.27018392  0.07670325]
 [ 0.1154149   0.26996102  0.9559291 ]
 [-0.60984466  0.07009174  0.78941538]
 [-0.98237224  0.09391583  0.16163104]
 [-0.84609345  0.06482304  0.5290783 ]
 [-0.22448816  0.53299048  0.8157979 ]
 [ 0.12146282 -0.99224489  0.02639829]
 [ 0.19591098 -0.86261727  0.46638004]
 [-0.81558403 -0.54079301  0.20582907]
 [-0.25885426 -0.90287368  0.34323984]
 [ 0.53492121 -0.02637249  0.84449026]
 [ 0.53964131  0.43449257  0.72111266]
 [-0.19449693 -0.6806217   0.70634626]
 [-0.98053881 -0.15801018  0.11651794]
 [-0.7317953  -0.30771257  0.60810248]
 [-0.52046223 -0.33241611  0.78652311]
 [ 0.21408979  0.80786826  0.54910331]
 [-0.93116942  0.16113451  0.32704613]
 [ 0.35270264  0.63898144  0.68359606]
 [ 0.69371315  0.46840791  0.54713445]
 [ 0.68109784 -0.53997035  0.4945076 ]
 [ 0.16962453 -0.72131562  0.67151418]
 [-0.00393353 -0.41503663  0.9097962 ]
 [ 0.87506372  0.34938832  0.33494968]
 [ 0.9594481  -0.08153172  0.26983683]
 [-0.06967638  0.06917517  0.99516833]
 [-0.50608658 -0.10979243  0.85546595]
 [ 0.          0.          0.        ]]

Both b-values and b-vectors look correct. Let’s now create the GradientTable.

gtab = gradient_table(bvals, bvecs=bvecs)

scene.clear()

We can also visualize the gradients. Let’s color the first shell blue and the second shell cyan.

colors_b1000 = window.colors.blue * np.ones(vertices.shape)
colors_b2500 = window.colors.cyan * np.ones(vertices.shape)
colors = np.vstack((colors_b1000, colors_b2500))
colors = np.insert(colors, (0, colors.shape[0]), np.array([0, 0, 0]), axis=0)
colors = np.ascontiguousarray(colors)

scene.add(actor.point(gtab.gradients, colors, point_radius=100))

window.record(scene=scene, out_path="gradients.png", size=(300, 300))
if interactive:
    window.show(scene)

Diffusion gradients.

References

[1]

Derek K. Jones, Mark A. Horsfield, and Andrew Simmons. Optimal strategies for measuring diffusion in anisotropic systems by magnetic resonance imaging. Magnetic Resonance in Medicine, 42(3):515–25, 1999. URL: http://www.ncbi.nlm.nih.gov/pubmed/10467296, doi:10.1002/(SICI)1522-2594(199909)42:3<515::AID-MRM14>3.0.CO;2-Q.