Reconstruct with Diffusion Spectrum Imaging (DSI)

We show how to apply Diffusion Spectrum Imaging [1] to diffusion MRI datasets of Cartesian keyhole diffusion gradients.

First import the necessary modules:

import matplotlib.pyplot as plt
import numpy as np

from dipy.core.gradients import gradient_table
from dipy.core.ndindex import ndindex
from dipy.data import get_fnames, get_sphere
from dipy.io.gradients import read_bvals_bvecs
from dipy.io.image import load_nifti
from dipy.reconst.dsi import DiffusionSpectrumModel
from dipy.reconst.odf import gfa

Download and get the data filenames for this tutorial.

fraw, fbval, fbvec = get_fnames(name="taiwan_ntu_dsi")

img contains a nibabel Nifti1Image object (data) and gtab contains a GradientTable object (gradient information e.g. b-values). For example to read the b-values it is possible to write print(gtab.bvals).

Load the raw diffusion data and the affine.

data, affine, voxel_size = load_nifti(fraw, return_voxsize=True)
bvals, bvecs = read_bvals_bvecs(fbval, fbvec)
bvecs[1:] = bvecs[1:] / np.sqrt(np.sum(bvecs[1:] * bvecs[1:], axis=1))[:, None]
gtab = gradient_table(bvals, bvecs=bvecs)
print(f"data.shape {data.shape}")

data.shape (96, 96, 60, 203)

This dataset has anisotropic voxel sizes, therefore reslicing is necessary.

Instantiate the Model and apply it to the data.

dsmodel = DiffusionSpectrumModel(gtab)

Let’s just use one slice only from the data.

dataslice = data[:, :, data.shape[2] // 2]

dsfit = dsmodel.fit(dataslice)

Load an odf reconstruction sphere

sphere = get_sphere(name="repulsion724")

Calculate the ODFs with this specific sphere

ODF = dsfit.odf(sphere)

print(f"ODF.shape {ODF.shape}")

/opt/homebrew/Caskroom/miniforge/base/envs/py312-test/lib/python3.12/site-packages/dipy/reconst/dsi.py:172: RuntimeWarning: invalid value encountered in divide
  Pr /= Pr.sum()
ODF.shape (96, 96, 724)

In a similar fashion it is possible to calculate the PDFs of all voxels in one call with the following way

PDF = dsfit.pdf()

print(f"PDF.shape {PDF.shape}")

PDF.shape (96, 96, 17, 17, 17)

We see that even for a single slice this PDF array is close to 345 MBytes so we really have to be careful with memory usage when use this function with a full dataset.

The simple solution is to generate/analyze the ODFs/PDFs by iterating through each voxel and not store them in memory if that is not necessary.

for index in ndindex(dataslice.shape[:2]):
    pdf = dsmodel.fit(dataslice[index]).pdf()

If you really want to save the PDFs of a full dataset on the disc we recommend using memory maps (numpy.memmap) but still have in mind that even if you do that for example for a dataset of volume size (96, 96, 60) you will need about 2.5 GBytes which can take less space when reasonable spheres (with < 1000 vertices) are used.

Let’s now calculate a map of Generalized Fractional Anisotropy (GFA) [2] using the DSI ODFs.

GFA = gfa(ODF)

fig_hist, ax = plt.subplots(1)
ax.set_axis_off()
plt.imshow(GFA.T)
plt.savefig("dsi_gfa.png", bbox_inches="tight")

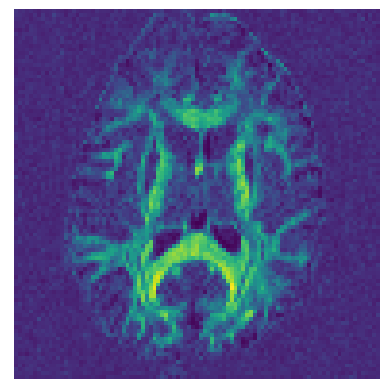
See also Calculate DSI-based scalar maps for calculating different types of DSI maps.

References

[1]

Van Jay Wedeen, Patric Hagmann, Wen-Yih Tseng, Timothy G. Reese, and Robert M. Weisskoff. Mapping Complex Tissue Architecture with Diffusion Spectrum Magnetic Resonance Imaging. Magnetic Resonance in Medicine, 54(6):1377–1386, 2005. URL: https://doi.org/10.1002/mrm.20642, doi:10.1002/mrm.20642.

[2]

David S. Tuch. Q-ball imaging. Magnetic Resonance in Medicine, 52(6):1358–1372, 2004. URL: https://doi.org/10.1002/mrm.20279, doi:10.1002/mrm.20279.