Reconstruction of the diffusion signal with the WMTI model (DKI-MICRO)

DKI can also be used to derive concrete biophysical parameters by applying microstructural models to DT and KT estimated from DKI. For instance, Fieremans et al.[1] showed that DKI can be used to estimate the contribution of hindered and restricted diffusion for well-aligned fibers - a model that was later referred to as the white matter tract integrity (WMTI) technique [2]. The two tensors of WMTI can be also interpreted as the influences of intra- and extra-cellular compartments and can be used to estimate the axonal volume fraction and diffusion extra-cellular tortuosity. According to previous studies [3], [2] these latter measures can be used to distinguish processes of axonal loss from processes of myelin degeneration. Details on the implementation of WMTI in DIPY are described in [4].

In this example, we show how to process a dMRI dataset using the WMTI model.

First, we import all relevant modules:

import matplotlib.pyplot as plt
import numpy as np
from scipy.ndimage import gaussian_filter

from dipy.core.gradients import gradient_table
from dipy.data import get_fnames
from dipy.io.gradients import read_bvals_bvecs
from dipy.io.image import load_nifti
import dipy.reconst.dki as dki
import dipy.reconst.dki_micro as dki_micro
from dipy.segment.mask import median_otsu

As the standard DKI, WMTI requires multi-shell data, i.e. data acquired from more than one non-zero b-value. Here, we use a fetcher to download a multi-shell dataset which was kindly provided by Hansen and Jespersen (more details about the data are provided in their paper [5]).

fraw, fbval, fbvec, t1_fname = get_fnames(name="cfin_multib")

data, affine = load_nifti(fraw)
bvals, bvecs = read_bvals_bvecs(fbval, fbvec)
gtab = gradient_table(bvals, bvecs=bvecs)

For comparison, this dataset is pre-processed using the same steps used in the example for reconstructing DKI (see Reconstruction of the diffusion signal with the kurtosis tensor model (DKI)).

# data masking
maskdata, mask = median_otsu(
    data, vol_idx=[0, 1], median_radius=4, numpass=2, autocrop=False, dilate=1
)

# Smoothing
fwhm = 1.25
gauss_std = fwhm / np.sqrt(8 * np.log(2))
data_smooth = np.zeros(data.shape)
for v in range(data.shape[-1]):
    data_smooth[..., v] = gaussian_filter(data[..., v], sigma=gauss_std)

The WMTI model can be defined in DIPY by instantiating the ‘KurtosisMicrostructureModel’ object in the following way:

dki_micro_model = dki_micro.KurtosisMicrostructureModel(gtab)

Before fitting this microstructural model, it is useful to indicate the regions in which this model provides meaningful information (i.e. voxels of well-aligned fibers). Following Fieremans et al.[1], a simple way to select this region is to generate a well-aligned fiber mask based on the values of diffusion sphericity, planarity and linearity. Here we will follow these selection criteria for a better comparison of our figures with the original article published by Fieremans et al.[1]. Nevertheless, it is important to note that voxels with well-aligned fibers can be selected based on other approaches such as using predefined regions of interest.

# Diffusion Tensor is computed based on the standard DKI model
dkimodel = dki.DiffusionKurtosisModel(gtab)
dkifit = dkimodel.fit(data_smooth, mask=mask)

# Initialize well aligned mask with ones
well_aligned_mask = np.ones(data.shape[:-1], dtype="bool")

# Diffusion coefficient of linearity (cl) has to be larger than 0.4, thus
# we exclude voxels with cl < 0.4.
cl = dkifit.linearity.copy()
well_aligned_mask[cl < 0.4] = False

# Diffusion coefficient of planarity (cp) has to be lower than 0.2, thus
# we exclude voxels with cp > 0.2.
cp = dkifit.planarity.copy()
well_aligned_mask[cp > 0.2] = False

# Diffusion coefficient of sphericity (cs) has to be lower than 0.35, thus
# we exclude voxels with cs > 0.35.
cs = dkifit.sphericity.copy()
well_aligned_mask[cs > 0.35] = False

# Removing nan associated with background voxels
well_aligned_mask[np.isnan(cl)] = False
well_aligned_mask[np.isnan(cp)] = False
well_aligned_mask[np.isnan(cs)] = False

Analogous to DKI, the data fit can be done by calling the fit function of the model’s object as follows:

dki_micro_fit = dki_micro_model.fit(data_smooth, mask=well_aligned_mask)

The KurtosisMicrostructureFit object created by this fit function can then be used to extract model parameters such as the axonal water fraction and diffusion hindered tortuosity:

AWF = dki_micro_fit.awf
TORT = dki_micro_fit.tortuosity

These parameters are plotted below on top of the mean kurtosis maps:

MK = dkifit.mk(min_kurtosis=0, max_kurtosis=3)

axial_slice = 9

fig1, ax = plt.subplots(1, 2, figsize=(9, 4), subplot_kw={"xticks": [], "yticks": []})

AWF[AWF == 0] = np.nan
TORT[TORT == 0] = np.nan

ax[0].imshow(
    MK[:, :, axial_slice].T, cmap=plt.cm.gray, interpolation="nearest", origin="lower"
)
im0 = ax[0].imshow(
    AWF[:, :, axial_slice].T,
    cmap=plt.cm.Reds,
    alpha=0.9,
    vmin=0.3,
    vmax=0.7,
    interpolation="nearest",
    origin="lower",
)
fig1.colorbar(im0, ax=ax.flat[0])

ax[1].imshow(
    MK[:, :, axial_slice].T, cmap=plt.cm.gray, interpolation="nearest", origin="lower"
)
im1 = ax[1].imshow(
    TORT[:, :, axial_slice].T,
    cmap=plt.cm.Blues,
    alpha=0.9,
    vmin=2,
    vmax=6,
    interpolation="nearest",
    origin="lower",
)
fig1.colorbar(im1, ax=ax.flat[1])

fig1.savefig("Kurtosis_Microstructural_measures.png")

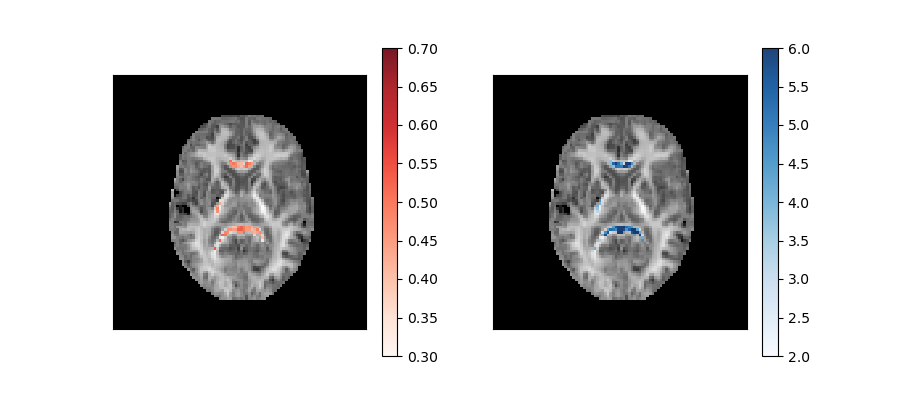
Axonal water fraction (left panel) and tortuosity (right panel) values of well-aligned fiber regions overlaid on a top of a mean kurtosis all-brain image.

References

[1] (1,2,3)

Els Fieremans, Jens H. Jensen, and Joseph A. Helpern. White matter characterization with diffusional kurtosis imaging. NeuroImage, 58(1):177–188, 2011. URL: https://doi.org/10.1016/j.neuroimage.2011.06.006, doi:10.1016/j.neuroimage.2011.06.006.

[2] (1,2)

Els Fieremans, Andreana Benitez, Jens H. Jensen, Maria F. Falangola, Ali Tabesh, Rachael L. Deardorff, Maria Vittoria S. Spampinato, James S. Babb, Dmitry S. Novikov, Steven H. Ferris, and Joseph A. Helpern. Novel White Matter Tract Integrity Metrics Sensitive to Alzheimer Disease Progression. American Journal of Neuroradiology, 34(11):2105–2112, 2013. URL: https://www.ajnr.org/content/34/11/2105, doi:10.3174/ajnr.A3553.

[3]

Els Fieremans, Jens H. Jensen, Joseph A. Helpern, Sungheon Kim, Robert I. Grossman, Matilde Inglese, and Dmitry S. Novikov. Diffusion distinguishes between axonal loss and demyelination in brain white matter. In ISMRM 20th Annual Meeting & Exhibition SMRT 21st Annual Meeting. Melbourne, Australia, 2012. International Society for Magnetic Resonance in Medicine (ISMRM).

[4]

Rafael Neto Henriques, Marta M. Correia, Maurizio Marrale, Elizabeth Huber, John Kruper, Serge Koudoro, Jason D. Yeatman, Eleftherios Garyfallidis, and Ariel Rokem. Diffusional Kurtosis Imaging in the Diffusion Imaging in Python Project. Frontiers in Human Neuroscience, July 2021. Sec. Brain Imaging and Stimulation. Advanced Diffusion MRI for Brain Microstructure: Methodology, Consistency, and Application. URL: https://doi.org/10.3389/fnhum.2021.675433, doi:10.3389/fnhum.2021.675433.

[5]

Brian Hansen and Sune Nørhøj Jespersen. Data for evaluation of fast kurtosis strategies, b-value optimization and exploration of diffusion MRI contrast. Scientific Data, 3(1):160072, August 2016. URL: https://doi.org/10.1038/sdata.2016.72, doi:10.1038/sdata.2016.72.