Denoise images using Non-Local Means (NLMEANS)

Using the non-local means filter [1] and [2] and you can denoise 3D or 4D images and boost the SNR of your datasets. You can also decide between modeling the noise as Gaussian or Rician (default).

We start by loading the necessary modules

from time import time

import matplotlib.pyplot as plt
import numpy as np

from dipy.data import get_fnames
from dipy.denoise.nlmeans import nlmeans
from dipy.denoise.noise_estimate import estimate_sigma
from dipy.io.image import load_nifti, save_nifti

Then, let’s fetch and load a T1 data from Stanford University

t1_fname = get_fnames(name="stanford_t1")
data, affine = load_nifti(t1_fname)

mask = data > 1500

print("vol size", data.shape)

vol size (81, 106, 76)

In order to call non_local_means first you need to estimate the standard deviation of the noise. We have used N=32 since the Stanford dataset was acquired on a 3T GE scanner with a 32 array head coil.

sigma = estimate_sigma(data, N=32)

Calling the main function non_local_means

t = time()

den = nlmeans(data, sigma=sigma, mask=mask, patch_radius=1, block_radius=2, rician=True)

print("total time", time() - t)

total time 0.07584619522094727

Let us plot the axial slice of the denoised output

axial_middle = data.shape[2] // 2

before = data[:, :, axial_middle].T
after = den[:, :, axial_middle].T

difference = np.abs(after.astype(np.float64) - before.astype(np.float64))

difference[~mask[:, :, axial_middle].T] = 0


fig, ax = plt.subplots(1, 3)
ax[0].imshow(before, cmap="gray", origin="lower")
ax[0].set_title("before")
ax[1].imshow(after, cmap="gray", origin="lower")
ax[1].set_title("after")
ax[2].imshow(difference, cmap="gray", origin="lower")
ax[2].set_title("difference")

plt.savefig("denoised.png", bbox_inches="tight")

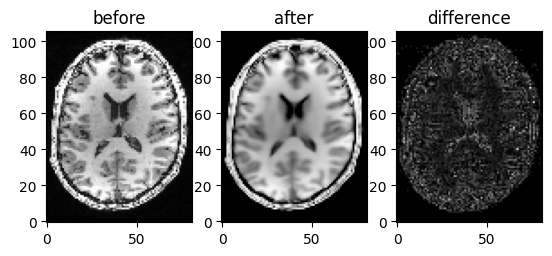
Showing axial slice before (left) and after (right) NLMEANS denoising

save_nifti("denoised.nii.gz", den, affine)

An improved version of non-local means denoising is adaptive soft coefficient matching, please refer to Denoise images using Adaptive Soft Coefficient Matching (ASCM) for more details.

References

[1]

Pierrick Coupé, Pierre Yger, Sylvain Prima, Pierre Hellier, Charles Kervrann, and Christian Barillot. An Optimized Blockwise Nonlocal Means Denoising Filter for 3-D Magnetic Resonance Images. IEEE Transactions on Medical Imaging, 27(4):425–441, 2008. URL: https://doi.org/10.1109/TMI.2008.2008967, doi:10.1109/TMI.2007.906087.

[2]

Pierrick Coupé, José V. Manjón, Montserrat Robles, and Louis D. Collins. Adaptive Multiresolution Non-Local Means Filter for 3D MR Image Denoising. IET Image Processing, 6(5):558–568, July 2012. URL: https://doi.org/10.1049/iet-ipr.2011.0161, doi:10.1049/iet-ipr.2011.0161.