Direct Bundle Registration

This example explains how you can register two bundles from two different subjects directly in the space of streamlines [1], [2].

To show the concept we will use two pre-saved cingulum bundles. The algorithm used here is called Streamline-based Linear Registration (SLR) [2].

from time import sleep

from dipy.align.streamlinear import StreamlineLinearRegistration
from dipy.data import two_cingulum_bundles
from dipy.tracking.streamline import set_number_of_points
from dipy.viz import actor, window

Let’s download and load the two bundles.

cb_subj1, cb_subj2 = two_cingulum_bundles()

An important step before running the registration is to resample the streamlines so that they both have the same number of points per streamline. Here we will use 20 points. This step is not optional. Inputting streamlines with a different number of points will break the theoretical advantages of using the SLR as explained in [2].

cb_subj1 = set_number_of_points(cb_subj1, nb_points=20)
cb_subj2 = set_number_of_points(cb_subj2, nb_points=20)

Let’s say now that we want to move the cb_subj2 (moving) so that it can be aligned with cb_subj1 (static). Here is how this is done.

srr = StreamlineLinearRegistration()

srm = srr.optimize(static=cb_subj1, moving=cb_subj2)

After the optimization is finished we can apply the transformation to cb_subj2.

cb_subj2_aligned = srm.transform(cb_subj2)


def show_both_bundles(bundles, colors=None, show=True, fname=None):
    scene = window.Scene()
    scene.SetBackground(1.0, 1, 1)
    for i, bundle in enumerate(bundles):
        color = colors[i]
        lines_actor = actor.streamtube(bundle, colors=color, linewidth=0.3)
        lines_actor.RotateX(-90)
        lines_actor.RotateZ(90)
        scene.add(lines_actor)
    if show:
        window.show(scene)
    if fname is not None:
        sleep(1)
        window.record(scene=scene, n_frames=1, out_path=fname, size=(900, 900))


show_both_bundles(
    [cb_subj1, cb_subj2],
    colors=[window.colors.orange, window.colors.red],
    show=False,
    fname="before_registration.png",
)

Before bundle registration.

show_both_bundles(
    [cb_subj1, cb_subj2_aligned],
    colors=[window.colors.orange, window.colors.red],
    show=False,
    fname="after_registration.png",
)

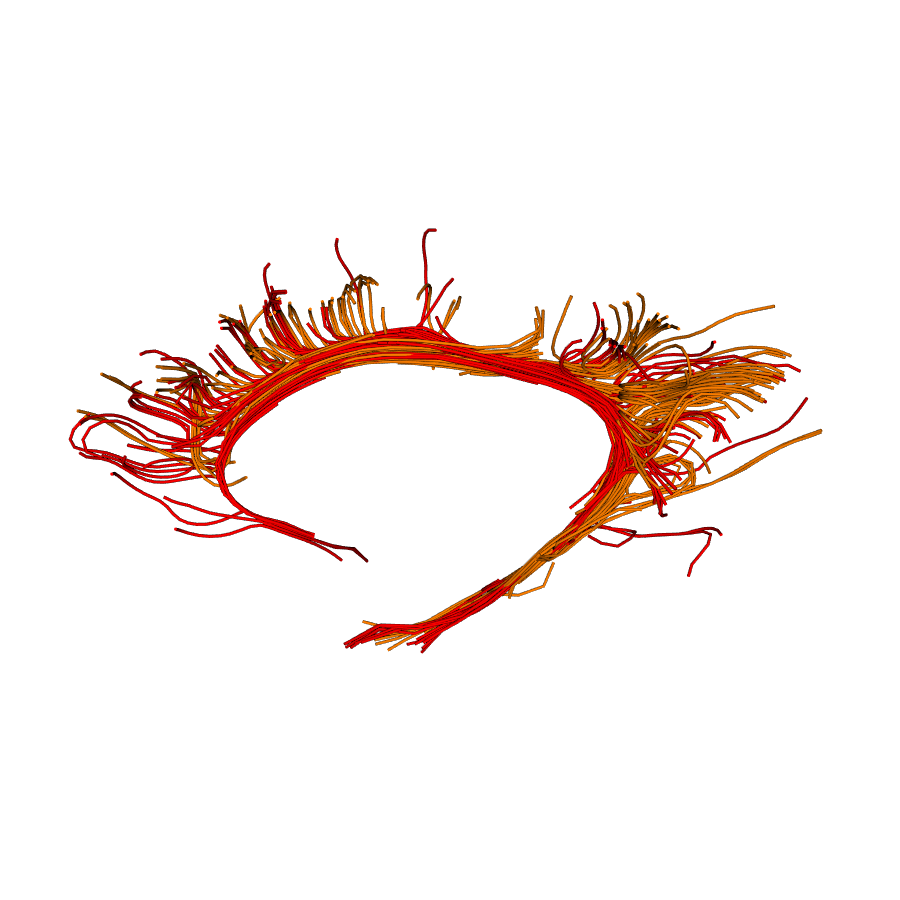
After bundle registration.

As you can see the two cingulum bundles are well aligned although they contain many streamlines of different lengths and shapes.

Streamline-based Linear Registration (SLR) is a method which given two sets of streamlines (fixed and moving) and a streamline-based cost function, will minimize the cost function and transform the moving set of streamlines (target) to the fixed (reference), so that they maximally overlap under the condition that the transform stays linear.

We denote a single streamline with s and a set of streamlines with S. A streamline s is an ordered sequence of line segments connecting 3D vector points \(\mathbf{x}_{k} \in \mathbb{R}^{3}\) with \(k \in[1, K]\) where K is the total number of points of streamline s. Given two bundles(two sets of streamlines), we denote \(S_{a}=\left\{s_{1}^{a}, \ldots, S_{A}^{a}\right\}\) and \(S_{b}=\left\{s_{1}^{b}, \ldots, s_{B}^{b}\right\}\), where A and B are the total numbers of streamlines in each set respectively. We want to minimize a cost function so that we can align the two sets together. For this purpose, we introduce a new cost function, the Bundle-based Minimum Distance (BMD), which is defined as:

\[\begin{split}\operatorname{BMD}\left(S_{a}, S_{b}\right)=\frac{1}{4}\left(\frac{1}{A} \sum_{i=1}^{A} \min _{j} D(i, j)+\frac{1}{B} \sum_{j=1}^{B} \\ \min _{i} D(i, j)\right)^{2}\end{split}\]

where D is the rectangular matrix given by all pairwise Minimum average Direct-Flip (MDF) streamline distances (Garyfallidis et al., 2012). Therefore, every element of matrix D is equal to \(D_{i j}=M D F\left(s^{a}{ }_{i}, s^{b}{ }_{j}\right)\).

Notice, how in Eq. (1), the most similar streamlines from one streamline set to the other are weighted more by averaging the minimum values of the rows and columns of matrix D. This makes our method robust to fanning streamlines near endpoints of bundles and spurious streamlines if any in the bundle. The MDF is a symmetric distance between two individual streamlines. It was primarily used for clustering (Garyfallidis et al., 2010; Visser et al., 2011) and tractography simplification (see Garyfallidis et al., 2012). This distance can be applied only when both streamlines have the same number of points. Therefore we assume from now on that an initial interpolation of streamlines has been applied, so that all streamlines have the same number of points K, and all segments of each streamline have equal length. The length of each segment is equal to the length of the streamline divided by the number of segments \((K-1)\). This is achieved by a simple linear interpolation with the starting and ending points of the streamlines intact. When K is small, the interpolation provides a rough representation of the streamline, but as K becomes larger and larger the shape of the interpolated streamline becomes identical with the shape of the initial streamline. Under this assumption, the MDF for two streamlines \(S_{a}\) and \(S_{b}\) is defined as:

\[\begin{split}\operatorname{MDF}\left(s_{i}^{a}, s_{j}^{b}\right)=\min \\ \left(d_{\text {direct }}\left(s_{i}^{a}, s_{j}^{b}\right), \\ d_{\text {flipped }}\left(s_{i}^{a}, s_{j}^{b}\right)\right)\end{split}\]

where \(d_{\text {direct }}\) is the direct distance which is defined as:

\[\begin{split}d_{\text {direct }}\left(s_{i}^{a}, s_{j}^{b}\right)=\frac{1}{K} \\ \sum_{k=1}^{K}\left\|\mathbf{x}_{k}^{a}-\mathbf{x}_{k}^{b}\right\|_{2}\end{split}\]

where \(x_{k}^{a}\) is the k-th point of streamline \(S_{i}^{a}\) and \(x_{k}^{b}\) is the k-th point of streamline \(S_{j}^{b}\). \(d_{\text {flipped }}\) is the one of the streamlines flipped and it is defined as:

\[\begin{split}d_{\text {flipped }}\left(s_{i}^{a}, s_{j}^{b}\right)=\frac{1}{K} \\ \sum_{k=1}^{K}\left\|\mathbf{x}_{k}^{a}-\mathbf{x}_{K-k+1}^{b}\\ \right\|_{2}\end{split}\]

and K is the total number of points in \(x^{a}\) and \(x^{b}\). The MDF has two very useful properties. First, it takes into consideration that streamlines have no preferred orientation. Second, it is a mathematically sound metric distance in the space of streamlines as proved in Garyfallidis et al. (2012). This means that the MDF is nonnegative, 0 only when both streamlines are identical, symmetric and it satisfies the triangle inequality. Now that we have defined our cost function in Eq. (1) we can formulate the following optimization problem. Given a fixed bundle S and a moving bundle M we would like to find the vector of parameters t which transforms M to S using a linear transformation T so that BMD is minimum:

\[\begin{split}\operatorname{SLR}(S, M)=\\underset{\mathbf{t}}{\operatorname{argmin}} \\ \operatorname{BMD}(S, T(M, \mathbf{t}))\end{split}\]

Here, \(\mathbf{t}\) is a vector in \(\mathbb{R}^{n}\) holding the parameters of the linear transform where n = 12 for affine or n = 6 for rigid registration. From this vector we can then compose the transformation matrix which is applied to all the points of bundle M.

References

[1]

Eleftherios Garyfallidis, Demian Wassermann, and Maxime Descoteaux. Direct native-space fiber bundle alignment for group comparisons. In Joint Annual Meeting ISMRM-ESMRMB 2014 SMRT 23rd Annual Meeting. Milan, Italy, May 2014. International Society for Magnetic Resonance in Medicine (ISMRM).

[2] (1,2,3)

Eleftherios Garyfallidis, Omar Ocegueda, Demian Wassermann, and Maxime Descoteaux. Robust and efficient linear registration of white-matter fascicles in the space of streamlines. NeuroImage, 117:124–140, August 2015. URL: https://doi.org/10.1016/j.neuroimage.2015.05.016, doi:10.1016/j.neuroimage.2015.05.016.