Note
Go to the end to download the full example code
Crossing invariant fiber response function with FORECAST model#
We show how to obtain a voxel specific response function in the form of axially symmetric tensor and the fODF using the FORECAST model from [Anderson2005] , [Kaden2016] and [Zucchelli2017].
First import the necessary modules:
import numpy as np
import matplotlib.pyplot as plt
from dipy.reconst.forecast import ForecastModel
from dipy.viz import actor, window
from dipy.data import fetch_hbn, get_sphere
import nibabel as nib
import os.path as op
from dipy.core.gradients import gradient_table
Download and read the data for this tutorial. Our implementation of FORECAST requires multi-shell data.fetch_hbn() provides data that was acquired using b-values of 1000 and 2000 as part of the Healthy Brain Network study [Alexander2017] and was preprocessed and quality controlled in the HBN-POD2 dataset [RichieHalford2022].
data_path = fetch_hbn(["NDARAA948VFH"])[1]
dwi_path = op.join(
data_path, "derivatives", "qsiprep", "sub-NDARAA948VFH",
"ses-HBNsiteRU", "dwi")
img = nib.load(op.join(
dwi_path,
"sub-NDARAA948VFH_ses-HBNsiteRU_acq-64dir_space-T1w_desc-preproc_dwi.nii.gz"))
gtab = gradient_table(
op.join(dwi_path,
"sub-NDARAA948VFH_ses-HBNsiteRU_acq-64dir_space-T1w_desc-preproc_dwi.bval"),
op.join(dwi_path,
"sub-NDARAA948VFH_ses-HBNsiteRU_acq-64dir_space-T1w_desc-preproc_dwi.bvec"))
data = np.asarray(img.dataobj)
mask_img = nib.load(
op.join(dwi_path,
"sub-NDARAA948VFH_ses-HBNsiteRU_acq-64dir_space-T1w_desc-brain_mask.nii.gz"))
brain_mask = mask_img.get_fdata()
Let us consider only a single slice for the FORECAST fitting
data_small = data[:, :, 50:51]
mask_small = brain_mask[:, :, 50:51]
Instantiate the FORECAST Model.
“sh_order_max” is the spherical harmonics order (l) used for the fODF.
dec_alg is the spherical deconvolution algorithm used for the FORECAST basis fitting, in this case we used the Constrained Spherical Deconvolution (CSD) algorithm.
fm = ForecastModel(gtab, sh_order_max=6, dec_alg='CSD')
Fit the FORECAST to the data
0%| | 0/5148.0 [00:00<?, ?it/s]
0%|▌ | 20/5148.0 [00:00<00:26, 190.04it/s]
1%|█▍ | 54/5148.0 [00:00<00:19, 262.51it/s]
2%|██▍ | 92/5148.0 [00:00<00:16, 301.64it/s]
2%|███▎ | 127/5148.0 [00:00<00:16, 308.47it/s]
3%|████▏ | 163/5148.0 [00:00<00:15, 316.23it/s]
4%|█████▏ | 201/5148.0 [00:00<00:15, 326.86it/s]
5%|██████▏ | 239/5148.0 [00:00<00:14, 333.60it/s]
5%|███████▏ | 277/5148.0 [00:00<00:14, 338.00it/s]
6%|████████▏ | 313/5148.0 [00:00<00:14, 341.23it/s]
7%|█████████ | 349/5148.0 [00:01<00:13, 346.51it/s]
8%|██████████▏ | 389/5148.0 [00:01<00:13, 352.92it/s]
8%|███████████▏ | 429/5148.0 [00:01<00:13, 356.98it/s]
9%|████████████▎ | 471/5148.0 [00:01<00:12, 365.28it/s]
10%|█████████████▏ | 508/5148.0 [00:01<00:13, 356.58it/s]
11%|██████████████▎ | 548/5148.0 [00:01<00:12, 359.35it/s]
11%|███████████████▎ | 589/5148.0 [00:01<00:12, 364.03it/s]
12%|████████████████▎ | 629/5148.0 [00:01<00:12, 364.53it/s]
13%|█████████████████▍ | 669/5148.0 [00:01<00:12, 363.68it/s]
14%|██████████████████▍ | 707/5148.0 [00:02<00:12, 363.18it/s]
14%|███████████████████▎ | 744/5148.0 [00:02<00:12, 352.93it/s]
15%|████████████████████▎ | 781/5148.0 [00:02<00:12, 348.57it/s]
16%|█████████████████████▍ | 822/5148.0 [00:02<00:12, 356.46it/s]
17%|██████████████████████▎ | 859/5148.0 [00:02<00:11, 358.07it/s]
18%|███████████████████████▌ | 903/5148.0 [00:02<00:11, 375.35it/s]
18%|████████████████████████▌ | 943/5148.0 [00:02<00:11, 372.38it/s]
19%|█████████████████████████▊ | 990/5148.0 [00:02<00:10, 389.79it/s]
20%|██████████████████████████▌ | 1030/5148.0 [00:02<00:10, 382.53it/s]
21%|███████████████████████████▋ | 1073/5148.0 [00:03<00:10, 395.49it/s]
22%|████████████████████████████▊ | 1116/5148.0 [00:03<00:10, 390.09it/s]
23%|█████████████████████████████▉ | 1161/5148.0 [00:03<00:10, 396.65it/s]
23%|███████████████████████████████ | 1201/5148.0 [00:03<00:10, 387.29it/s]
24%|████████████████████████████████▏ | 1248/5148.0 [00:03<00:09, 400.09it/s]
25%|█████████████████████████████████▎ | 1289/5148.0 [00:03<00:09, 398.48it/s]
26%|██████████████████████████████████▍ | 1332/5148.0 [00:03<00:09, 403.83it/s]
27%|███████████████████████████████████▋ | 1382/5148.0 [00:03<00:08, 420.15it/s]
28%|████████████████████████████████████▊ | 1426/5148.0 [00:03<00:08, 414.71it/s]
29%|██████████████████████████████████████ | 1474/5148.0 [00:03<00:08, 422.04it/s]
29%|███████████████████████████████████████▏ | 1517/5148.0 [00:04<00:08, 416.13it/s]
30%|████████████████████████████████████████▍ | 1564/5148.0 [00:04<00:08, 421.84it/s]
31%|█████████████████████████████████████████▋ | 1612/5148.0 [00:04<00:08, 427.12it/s]
32%|██████████████████████████████████████████▉ | 1662/5148.0 [00:04<00:07, 436.28it/s]
33%|████████████████████████████████████████████ | 1706/5148.0 [00:04<00:08, 408.42it/s]
34%|█████████████████████████████████████████████▏ | 1751/5148.0 [00:04<00:08, 405.08it/s]
35%|██████████████████████████████████████████████▎ | 1793/5148.0 [00:04<00:08, 403.14it/s]
36%|███████████████████████████████████████████████▍ | 1836/5148.0 [00:04<00:08, 400.16it/s]
36%|████████████████████████████████████████████████▍ | 1877/5148.0 [00:04<00:08, 392.63it/s]
37%|█████████████████████████████████████████████████▋ | 1925/5148.0 [00:05<00:07, 406.42it/s]
38%|██████████████████████████████████████████████████▊ | 1966/5148.0 [00:05<00:07, 401.64it/s]
39%|████████████████████████████████████████████████████▏ | 2019/5148.0 [00:05<00:07, 421.74it/s]
40%|█████████████████████████████████████████████████████▍ | 2067/5148.0 [00:05<00:07, 426.85it/s]
41%|██████████████████████████████████████████████████████▋ | 2118/5148.0 [00:05<00:06, 438.61it/s]
42%|████████████████████████████████████████████████████████ | 2169/5148.0 [00:05<00:06, 446.60it/s]
43%|█████████████████████████████████████████████████████████▍ | 2223/5148.0 [00:05<00:06, 456.23it/s]
44%|██████████████████████████████████████████████████████████▋ | 2271/5148.0 [00:05<00:06, 451.06it/s]
45%|███████████████████████████████████████████████████████████▊ | 2317/5148.0 [00:05<00:06, 441.94it/s]
46%|█████████████████████████████████████████████████████████████▏ | 2366/5148.0 [00:06<00:06, 451.51it/s]
47%|██████████████████████████████████████████████████████████████▎ | 2412/5148.0 [00:06<00:06, 436.02it/s]
48%|███████████████████████████████████████████████████████████████▌ | 2461/5148.0 [00:06<00:06, 442.59it/s]
49%|████████████████████████████████████████████████████████████████▊ | 2509/5148.0 [00:06<00:05, 441.59it/s]
50%|██████████████████████████████████████████████████████████████████▏ | 2564/5148.0 [00:06<00:05, 460.00it/s]
51%|███████████████████████████████████████████████████████████████████▌ | 2616/5148.0 [00:06<00:05, 464.64it/s]
52%|████████████████████████████████████████████████████████████████████▉ | 2669/5148.0 [00:06<00:05, 482.37it/s]
53%|██████████████████████████████████████████████████████████████████████▍ | 2725/5148.0 [00:06<00:04, 495.26it/s]
54%|███████████████████████████████████████████████████████████████████████▋ | 2775/5148.0 [00:06<00:04, 483.58it/s]
55%|████████████████████████████████████████████████████████████████████████▉ | 2824/5148.0 [00:07<00:04, 472.81it/s]
56%|██████████████████████████████████████████████████████████████████████████▏ | 2872/5148.0 [00:07<00:05, 447.88it/s]
57%|███████████████████████████████████████████████████████████████████████████▍ | 2919/5148.0 [00:07<00:04, 450.70it/s]
58%|████████████████████████████████████████████████████████████████████████████▌ | 2965/5148.0 [00:07<00:04, 452.84it/s]
59%|█████████████████████████████████████████████████████████████████████████████▊ | 3012/5148.0 [00:07<00:04, 445.90it/s]
60%|███████████████████████████████████████████████████████████████████████████████▏ | 3066/5148.0 [00:07<00:04, 460.43it/s]
61%|████████████████████████████████████████████████████████████████████████████████▌ | 3118/5148.0 [00:07<00:04, 464.97it/s]
61%|█████████████████████████████████████████████████████████████████████████████████▊ | 3165/5148.0 [00:07<00:04, 465.32it/s]
63%|███████████████████████████████████████████████████████████████████████████████████▏ | 3218/5148.0 [00:07<00:04, 473.08it/s]
64%|████████████████████████████████████████████████████████████████████████████████████▌ | 3275/5148.0 [00:08<00:03, 487.75it/s]
65%|█████████████████████████████████████████████████████████████████████████████████████▉ | 3324/5148.0 [00:08<00:03, 483.20it/s]
66%|███████████████████████████████████████████████████████████████████████████████████████▏ | 3376/5148.0 [00:08<00:03, 480.97it/s]
67%|████████████████████████████████████████████████████████████████████████████████████████▍ | 3425/5148.0 [00:08<00:03, 476.73it/s]
67%|█████████████████████████████████████████████████████████████████████████████████████████▋ | 3473/5148.0 [00:08<00:03, 459.33it/s]
69%|███████████████████████████████████████████████████████████████████████████████████████████▏ | 3529/5148.0 [00:08<00:03, 475.32it/s]
70%|████████████████████████████████████████████████████████████████████████████████████████████▌ | 3583/5148.0 [00:08<00:03, 480.85it/s]
71%|██████████████████████████████████████████████████████████████████████████████████████████████ | 3639/5148.0 [00:08<00:03, 490.22it/s]
72%|███████████████████████████████████████████████████████████████████████████████████████████████▎ | 3690/5148.0 [00:08<00:02, 494.20it/s]
73%|████████████████████████████████████████████████████████████████████████████████████████████████▌ | 3740/5148.0 [00:08<00:02, 487.78it/s]
74%|█████████████████████████████████████████████████████████████████████████████████████████████████▉ | 3790/5148.0 [00:09<00:02, 478.41it/s]
75%|███████████████████████████████████████████████████████████████████████████████████████████████████▏ | 3838/5148.0 [00:09<00:02, 471.38it/s]
75%|████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 3886/5148.0 [00:09<00:02, 461.45it/s]
76%|█████████████████████████████████████████████████████████████████████████████████████████████████████▌ | 3933/5148.0 [00:09<00:02, 446.87it/s]
77%|██████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 3984/5148.0 [00:09<00:02, 457.51it/s]
78%|████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 4038/5148.0 [00:09<00:02, 468.75it/s]
79%|█████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 4090/5148.0 [00:09<00:02, 470.76it/s]
80%|██████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 4139/5148.0 [00:09<00:02, 463.91it/s]
81%|████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 4195/5148.0 [00:09<00:02, 473.37it/s]
83%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 4249/5148.0 [00:10<00:01, 479.44it/s]
83%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 4297/5148.0 [00:10<00:01, 452.47it/s]
84%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 4346/5148.0 [00:10<00:01, 451.37it/s]
85%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 4392/5148.0 [00:10<00:01, 447.61it/s]
86%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 4439/5148.0 [00:10<00:01, 436.95it/s]
87%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 4493/5148.0 [00:10<00:01, 453.93it/s]
88%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 4548/5148.0 [00:10<00:01, 468.49it/s]
89%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 4595/5148.0 [00:10<00:01, 456.92it/s]
90%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 4641/5148.0 [00:10<00:01, 448.44it/s]
91%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 4692/5148.0 [00:11<00:00, 465.16it/s]
92%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 4740/5148.0 [00:11<00:00, 462.99it/s]
93%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 4793/5148.0 [00:11<00:00, 469.89it/s]
94%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏ | 4847/5148.0 [00:11<00:00, 477.15it/s]
95%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▍ | 4895/5148.0 [00:11<00:00, 469.35it/s]
96%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▉ | 4950/5148.0 [00:11<00:00, 475.42it/s]
97%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 5005/5148.0 [00:11<00:00, 483.67it/s]
98%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▊ | 5061/5148.0 [00:11<00:00, 492.19it/s]
99%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████ | 5111/5148.0 [00:11<00:00, 481.65it/s]
100%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 5148/5148.0 [00:12<00:00, 428.08it/s]
Calculate the crossing invariant tensor indices [Kaden2016] : the parallel diffusivity, the perpendicular diffusivity, the fractional anisotropy and the mean diffusivity.
d_par = f_fit.dpar
d_perp = f_fit.dperp
fa = f_fit.fractional_anisotropy()
md = f_fit.mean_diffusivity()
Show the indices and save them in FORECAST_indices.png.
fig = plt.figure(figsize=(6, 6))
ax1 = fig.add_subplot(2, 2, 1, title='parallel diffusivity')
ax1.set_axis_off()
ind = ax1.imshow(d_par[:, :, 0].T, interpolation='nearest',
origin='lower', cmap=plt.cm.gray)
plt.colorbar(ind, shrink=0.6)
ax2 = fig.add_subplot(2, 2, 2, title='perpendicular diffusivity')
ax2.set_axis_off()
ind = ax2.imshow(d_perp[:, :, 0].T, interpolation='nearest',
origin='lower', cmap=plt.cm.gray)
plt.colorbar(ind, shrink=0.6)
ax3 = fig.add_subplot(2, 2, 3, title='fractional anisotropy')
ax3.set_axis_off()
ind = ax3.imshow(fa[:, :, 0].T, interpolation='nearest',
origin='lower', cmap=plt.cm.gray)
plt.colorbar(ind, shrink=0.6)
ax4 = fig.add_subplot(2, 2, 4, title='mean diffusivity')
ax4.set_axis_off()
ind = ax4.imshow(md[:, :, 0].T, interpolation='nearest',
origin='lower', cmap=plt.cm.gray)
plt.colorbar(ind, shrink=0.6)
plt.savefig('FORECAST_indices.png', dpi=300, bbox_inches='tight')
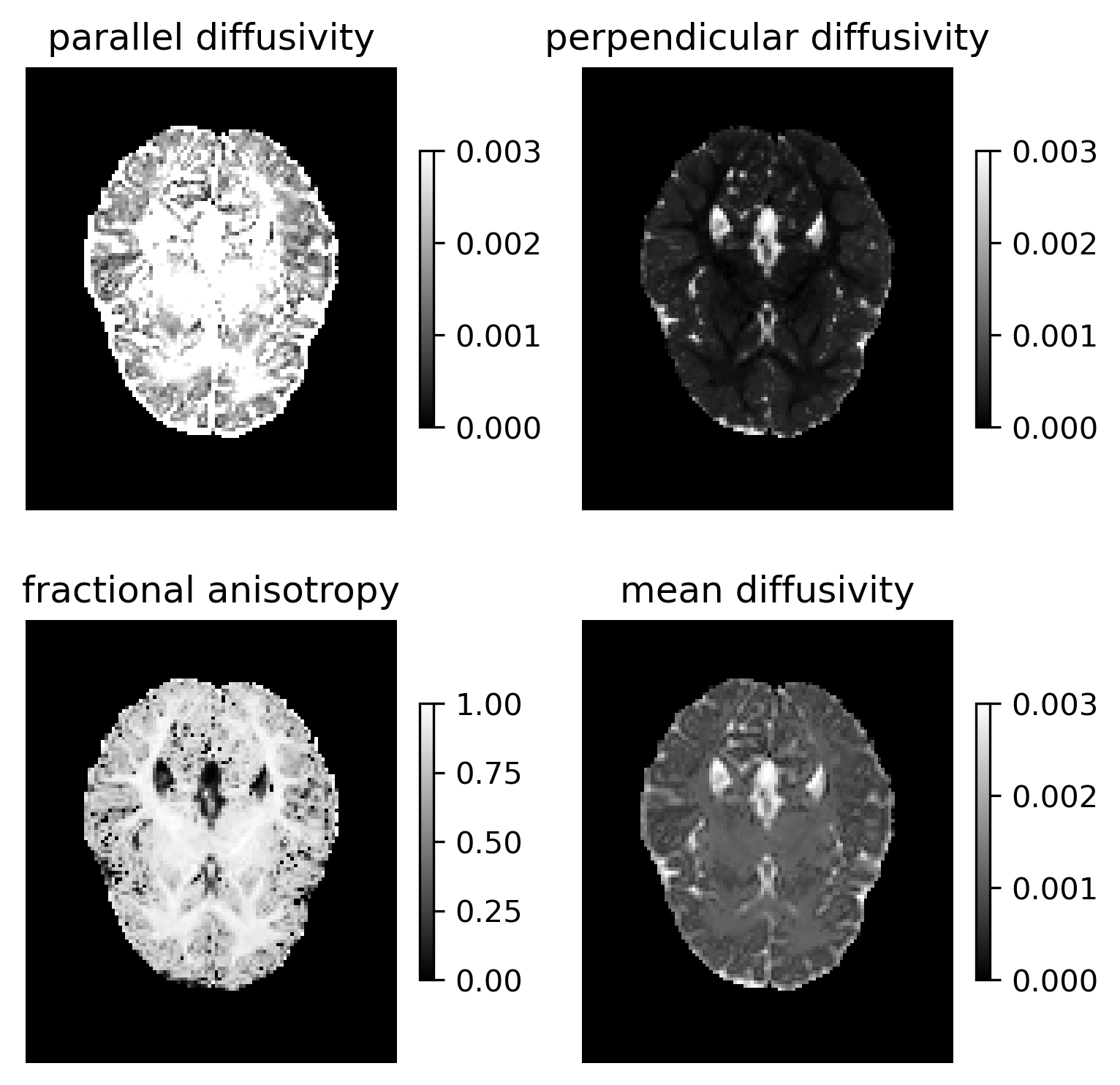
FORECAST scalar indices.
Load an ODF reconstruction sphere
sphere = get_sphere('repulsion724')
Compute the fODFs.
fODF.shape (108, 129, 1, 724)
Display a part of the fODFs
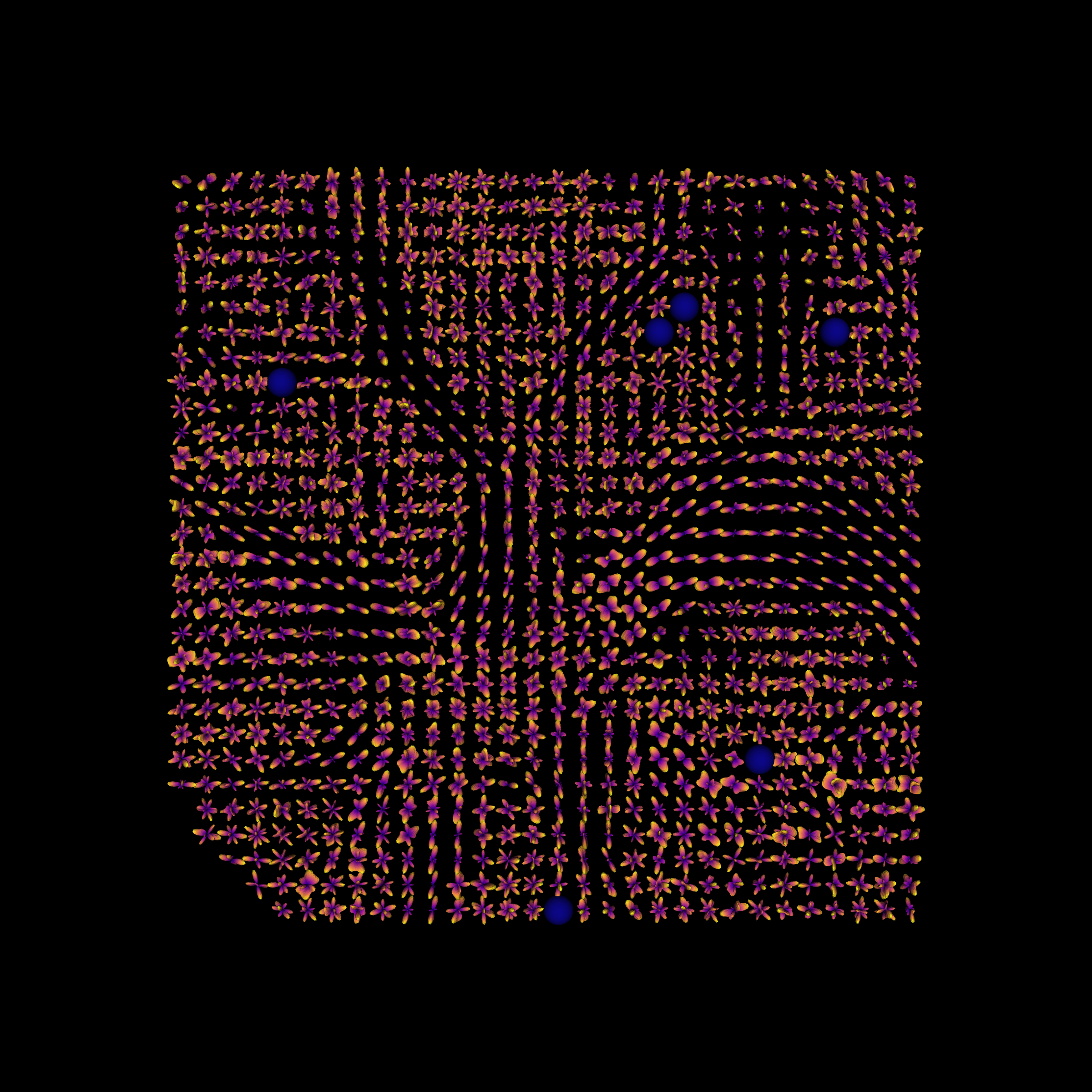
Fiber Orientation Distribution Functions, in a small ROI of the brain.
References#
[Anderson2005]
Anderson A. W., “Measurement of Fiber Orientation Distributions Using High Angular Resolution Diffusion Imaging”, Magnetic Resonance in Medicine, 2005.
[Kaden2016]
(1,2)
Kaden E. et al., “Quantitative Mapping of the Per-Axon Diffusion Coefficients in Brain White Matter”, Magnetic Resonance in Medicine, 2016.
[Zucchelli2017]
Zucchelli E. et al., “A generalized SMT-based framework for Diffusion MRI microstructural model estimation”, MICCAI Workshop on Computational DIFFUSION MRI (CDMRI), 2017.
[Alexander2017]
Alexander LM, Escalera J, Ai L, et al. An open resource for transdiagnostic research in pediatric mental health and learning disorders. Sci Data. 2017;4:170181.
[RichieHalford2022]
Richie-Halford A, Cieslak M, Ai L, et al. An analysis-ready and quality controlled resource for pediatric brain white-matter research. Scientific Data. 2022;9(1):1-27.
Total running time of the script: (1 minutes 3.197 seconds)